Question

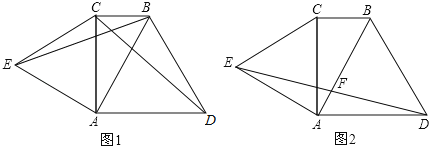
【题目】已知，Rt△ABC中，∠ACB=90°，∠CAB=30°．分别以AB、AC为边，向三角形外作等边△ABD和等边△ACE．

（1）如图1，连接线段BE、CD．求证：BE=CD；

（2）如图2，连接DE交AB于点F．求证：F为DE中点．

Answer 1

【答案】(1)证明见解析(2)证明见解析

【解析】此题考查了全等三角形的判定与性质，平行线的性质，以及等边三角形的性质，

（1）由△ABD和△ACE是等边三角形，根据等边三角形的性质得到AB=AD，AC=AE，∠DAB=∠EAC=60°，然后给∠DAB和∠EAC都加上∠BAC，得到∠DAC=∠BAE，利用“SAS“即可得到△DAC≌△BAE，最后根据全等三角形的对应边相等即可得证；

（2）作DG∥AE，交AB于点G，由等边三角形的∠EAC=60°，加上已知的∠CAB=30°得到∠FAE=90°，然后根据两直线平行内错角相等得到∠DGF=90°，再根据∠ACB=90°，∠CAB=30°，利用三角形的内角和定理得到∠ABC=60°，由等边三角形的性质也得到∠DBG=60°，从而得到两角的相等，再由DB=AB，利用“AAS”证得△DGB≌△ACB，根据全等三角形的对应边相等得到DG=AC，再由△AEC为等边三角形得到AE=AC，等量代换可得DG=AE，加上一对对顶角的相等和一对直角的相等根据“AAS”证得△DGF≌△EAF，最后根据全等三角形的对应边相等即可得证．

（1）∵△ABD和△ACE是等边三角形，

∴AB=AD，AC=AE，∠DAB=∠EAC=60°，

∴∠DAB+∠BAC=∠EAC+∠BAC，即∠DAC=∠BAE，

在△DAC和△BAE中，

∴△DAC≌△BAE（SAS），

∴DC=BE；

（2）如图，作DG∥AE，交AB于点G，

由∠EAC=60°，∠CAB=30°得：∠FAE=∠EAC+∠CAB=90°，

∴∠DGF=∠FAE=90°，

又∵∠ACB=90°，∠CAB=30°，

∴∠ABC=60°，

又∵△ABD为等边三角形，∠DBG=60°，DB=AB，

∴∠DBG=∠ABC=60°，

在△DGB和△ACB中，

∴△DGB≌△ACB（AAS），

∴DG=AC，

又∵△AEC为等边三角形，∴AE=AC，

∴DG=AE，

在△DGF和△EAF中，

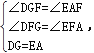
∴△DGF≌△EAF（AAS），

∴DF=EF，即F为DE中点．