【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.

参考答案:
【答案】(1)证明见解析;(2) (1)中的结论不成立,有DE=BF﹣EF,理由见解析.
【解析】试题分析:(1)由Rt△ABC≌Rt△ADE得AC=AE,根据HL可证得Rt△ACF≌Rt△AEF,由BC=BF+CF代入可得结论;
(2)如图②,(1)中的结论不成立,有DE=BF-EF,同(1):证明Rt△ACF≌Rt△AEF,再由BC=BF-FC得出结论.
试题解析:(1)如图①,连接AF,
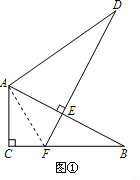
∵Rt△ABC≌Rt△ADE,
∴AC=AE,BC=DE,
∵∠ACB=∠AEF=90°,AF=AF,
∴Rt△ACF≌Rt△AEF,
∴CF=EF,
∴BF+EF=BF+CF=BC,
∴BF+EF=DE;
(2)如图②,(1)中的结论不成立,有DE=BF-EF,理由是:
连接AF,

∵Rt△ABC≌Rt△ADE,
∴AC=AE,BC=DE,
∵∠E=∠ACF=90°,AF=AF,
∴Rt△ACF≌Rt△AEF,
∴CF=EF,
∴DE=BC=BF-FC=BF-EF,
即DE=BF-EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b的图象经过第一、二、三象限且经过(0,2)点.任写一个满足上述条件的一次函数的表达式是_________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,∠ABC,∠ACB的平分线分别交AC、AB于点D,E,CE、BD相交于点F,连接DE.下列结论:①AB=BC;②∠BFE=60°;③CE
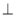 AB;④点F到△ABC三边的距离相等;⑤BE+CD=BC.其中正确的结论是__________________.
AB;④点F到△ABC三边的距离相等;⑤BE+CD=BC.其中正确的结论是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2)2+4÷(﹣2)×(3﹣5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,某市共接待海内外游客约567000人次,将567000用科学记数法表示为( )
A. 567×103 B. 56.7×104 C. 5.67×105 D. 0.567×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角∠AOB内部画1条射线,可得3个锐角,画2条不同的射线,可得6个锐角,画3条不同的射线,可得10个锐角……照此规律,画10条不同的射线,可得锐角多少个?
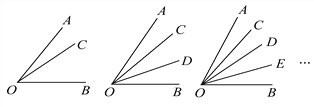
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱.现在有一个长为6cm,宽为5cm的长方形,分别绕它的长、宽所在直线旋转一周,得到不同的圆柱,它们的体积分别是多大?
相关试题

