【题目】把任意一个各个数位上的数字均不为0的多位自然数称为“完美数”,若将一个三位“完美数“的各数位上的数字两两组合,形成六个新的两位数,我们将这六个两位相加的和,叫做该三位“完美数”的“完美双和”,然后用所得的“完美双和”除以18,得到的结果记为![]() ,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,
,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,![]() 则:
则:
![]()
(1)填空:![]() ______;
______;
(2)证明:任意一个三位“完美数”的“完美双和”与该三位“完美数”各数位上数字之差能被21除;
(3)已知一个三位“完美数”![]() 其中
其中![]() ,
,![]() 且x,均为整数
且x,均为整数![]() ,满足百位数字与个位数字之和等于十位数字的2倍加1,求出
,满足百位数字与个位数字之和等于十位数字的2倍加1,求出![]() .
.
参考答案:
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
![]() 根据
根据![]() 的定义求解即可;
的定义求解即可;
![]() 设三位“完美数”百位数为a,十位数为b,个位数为c,计算出“完美双和”与该三位“完美数”各数位上数字之差,即可得证;
设三位“完美数”百位数为a,十位数为b,个位数为c,计算出“完美双和”与该三位“完美数”各数位上数字之差,即可得证;
![]() 根据“完美数”
根据“完美数”![]() 其中
其中![]() ,
,![]() 且x,均为整数
且x,均为整数![]() 是三位数,确定x的值,再根据这个三位数百位数字与个位数字之和等于十位数字的2倍加1,确定y的值,进而得出三个三位数,最后根据
是三位数,确定x的值,再根据这个三位数百位数字与个位数字之和等于十位数字的2倍加1,确定y的值,进而得出三个三位数,最后根据![]() 的定义求解即可.
的定义求解即可.
![]() 六个新数为51,15,53,35,13,31,则:
六个新数为51,15,53,35,13,31,则:![]() ;
;
![]() 三位“完美数”百位数为a,十位数为b,个位数为c,
三位“完美数”百位数为a,十位数为b,个位数为c,
则“完美双和”与该三位“完美数”各数位上数字之差为:![]() ,
,
![]() ,b,c为正整数,
,b,c为正整数,
![]() 一个三位“完美数”的“完美双和”与该三位“完美数”各数位上数字之差能被21除;
一个三位“完美数”的“完美双和”与该三位“完美数”各数位上数字之差能被21除;
![]() “完美数”
“完美数”![]() 其中
其中![]() ,
,![]() 且x,均为整数
且x,均为整数![]() 是三位数,
是三位数,
![]() 或
或![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 这个三位数百位数字与个位数字之和等于十位数字的2倍加1,
这个三位数百位数字与个位数字之和等于十位数字的2倍加1,
![]() ,解得
,解得![]() 舍去
舍去![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 这个三位数百位数字与个位数字之和等于十位数字的2倍加1,
这个三位数百位数字与个位数字之和等于十位数字的2倍加1,
![]() ,解得
,解得![]() ,
,
此时![]() ,
,
同![]() 的方法,可求得
的方法,可求得![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 这个三位数百位数字与个位数字之和等于十位数字的2倍加1,
这个三位数百位数字与个位数字之和等于十位数字的2倍加1,
![]() ,解得
,解得![]() ,
,
此时![]() ,
,
同![]() 的方法,可求得
的方法,可求得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年10月份某商场用19600元同时购进A、B两种新型节能日光灯共440盏,A型日光灯每盏进价为40元,售价为60元,B型日光灯每盏进价为50元,售价为80元.
(1)求10月份两种新型节能日光灯各购进多少盏?
(2)将10月份购买的日光灯从生产基地运往商场的过程中,A型日光灯出现
 的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润
的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润 型日光灯在原售价基础上提高
型日光灯在原售价基础上提高 ,问A型日光灯调整后的售价为多少元?
,问A型日光灯调整后的售价为多少元?(3)进入11月份,B型日光灯的需求量增大,于是商场在筹备“双十一”促销活动时,决定去甲、乙两个生产基地只购进一批B型日光灯,甲、乙生产基地给出了不同的优惠措施:
甲生产基地:B型日光灯出厂价为每盏50元,折扣如表一所示
乙生产基地:B型日光灯出厂价为每盏47元,同时当出厂总金额达一定数量后还可按表二返现金.
表一
甲生产基地
一次性购买的数量
折扣数
不超过150盏的部分
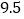 折
折超过150盏的部分
9折
表二
乙生产基地
出厂总金额
返现金
不超过5640元
0元
超过5640元,但不超过9353元
返现300元
超过9353元
先返现出厂总金额的
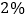 后,再返现206元
后,再返现206元已知该商场在甲生产基地购买B型日光灯共支付7350元,在乙生产基地购买B型日光灯共支付9006元,若将在两个生产基地购买的B型日光灯的总量改由在乙生产基地一次性购买,则支付总金额比在甲、乙两生产基地分别购买的支付金额之和可节约多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )
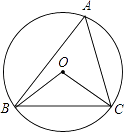
A.3
B.4
C.5
D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有2019条直线
 且有
且有 …,则直线
…,则直线 与
与 的位置关系是___________.
的位置关系是___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算:(3﹣π)0+4sin45°﹣ +|1﹣
+|1﹣  |
|
(2)化简求值:( +
+  )÷
)÷  ,其中x=6.
,其中x=6. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A.B两点都与平面镜相距4米,且A.B两点相距6米,一束光线由A射向平面镜反射之后恰巧经过B点.求B点到入射点的距离.
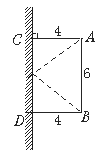
相关试题

