【题目】今年10月份某商场用19600元同时购进A、B两种新型节能日光灯共440盏,A型日光灯每盏进价为40元,售价为60元,B型日光灯每盏进价为50元,售价为80元.
(1)求10月份两种新型节能日光灯各购进多少盏?
(2)将10月份购买的日光灯从生产基地运往商场的过程中,A型日光灯出现![]() 的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润
的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润![]() 型日光灯在原售价基础上提高
型日光灯在原售价基础上提高![]() ,问A型日光灯调整后的售价为多少元?
,问A型日光灯调整后的售价为多少元?
(3)进入11月份,B型日光灯的需求量增大,于是商场在筹备“双十一”促销活动时,决定去甲、乙两个生产基地只购进一批B型日光灯,甲、乙生产基地给出了不同的优惠措施:
甲生产基地:B型日光灯出厂价为每盏50元,折扣如表一所示
乙生产基地:B型日光灯出厂价为每盏47元,同时当出厂总金额达一定数量后还可按表二返现金.
表一
甲生产基地 | |
一次性购买的数量 | 折扣数 |
不超过150盏的部分 |
|
超过150盏的部分 | 9折 |
表二
乙生产基地 | |
出厂总金额 | 返现金 |
不超过5640元 | 0元 |
超过5640元,但不超过9353元 | 返现300元 |
超过9353元 | 先返现出厂总金额的 |
已知该商场在甲生产基地购买B型日光灯共支付7350元,在乙生产基地购买B型日光灯共支付9006元,若将在两个生产基地购买的B型日光灯的总量改由在乙生产基地一次性购买,则支付总金额比在甲、乙两生产基地分别购买的支付金额之和可节约多少元?
参考答案:
【答案】(1)购进A型日光灯240盏,B型日光灯200盏;(2)A型日光灯调整后的价格为66元;(3)若将在两个生产基地购买的B型日光灯的总量改由在乙生产基地一次性购买,则支付总金额比在甲、乙两生产基地分别购买的支付金额之和可节302.82元.
【解析】
![]() 根据两种日光灯的总量是440,两种日光灯的总价是19600,可得方程组,即可得解;
根据两种日光灯的总量是440,两种日光灯的总价是19600,可得方程组,即可得解;
![]() 设A型日光灯调整后的价格为z元,根据全部售完后可获得10664元的利润,列出关于z的方程,计算即可;
设A型日光灯调整后的价格为z元,根据全部售完后可获得10664元的利润,列出关于z的方程,计算即可;
![]() 根据在甲生产基地支付7350元,在乙生产基地支付9006元,求的在甲、乙生产基地购买的日光灯的数量之和;此数量的日光灯在与由在乙生产基地一次性购买的所花费用进行比较.
根据在甲生产基地支付7350元,在乙生产基地支付9006元,求的在甲、乙生产基地购买的日光灯的数量之和;此数量的日光灯在与由在乙生产基地一次性购买的所花费用进行比较.
![]() 设购进A型日光灯x盏,B型日光灯(400﹣x)盏,
设购进A型日光灯x盏,B型日光灯(400﹣x)盏,
40x+50(400﹣x)=19600,
解得:x=240,
则B型日光灯有200盏,
答:购进A型日光灯240盏,B型日光灯200盏,
![]() 设A型日光灯调整后的价格为z元.
设A型日光灯调整后的价格为z元.
此时B型日光灯调整后的价格为![]() 元,
元,
![]() 可列方程为:
可列方程为:
![]() ,
,
解得:![]() ,
,
答:A型日光灯调整后的价格为66元;
![]() 解:
解:![]() ,
,
![]() 该商场在甲地购买的B型日光灯超过150台,
该商场在甲地购买的B型日光灯超过150台,
设该商场在甲地购买的B型日光灯m台,
则:![]() ,
,
解得:![]() ,
,
设该商场在乙地购买的B型日光灯n台,
![]() ,
,
解得:![]() ,
,
![]() ,
,
![]() 设该商场在甲、乙地购买的B型日光灯共353台,
设该商场在甲、乙地购买的B型日光灯共353台,
若设该商场只在乙地购买的B型日光灯,
则![]()
![]() 所花费用:
所花费用:![]() ,
,
节约的钱数:![]() ,
,
若将在两个生产基地购买的B型日光灯的总量改由在乙生产基地一次性购买,则支付总金额比在甲、乙两生产基地分别购买的支付金额之和可节约![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张的爸爸在上周星期六骑摩托车带小张和弟弟到离家27千米的游乐园玩耍,爸爸自己骑摩托车的速度为26千米
 时,由于摩托车后座只能搭乘一人,搭一人的速度为24千米
时,由于摩托车后座只能搭乘一人,搭一人的速度为24千米 时,当天三人同时从家出发,弟弟以4千米
时,当天三人同时从家出发,弟弟以4千米 时的速度步行,爸爸带小张骑摩托车行驶一定路程后,小张下车以6千米时的速度步行前往游乐园,爸爸返回接弟弟,接上弟弟后直接去游乐园排队买票,爸爸花了5分钟买好票,此时小张也正好到达、
时的速度步行,爸爸带小张骑摩托车行驶一定路程后,小张下车以6千米时的速度步行前往游乐园,爸爸返回接弟弟,接上弟弟后直接去游乐园排队买票,爸爸花了5分钟买好票,此时小张也正好到达、 爸爸骑摩托车掉头和停放摩托车的时间忽略不计
爸爸骑摩托车掉头和停放摩托车的时间忽略不计 问:小张搭乘摩托车的路程为______千米.
问:小张搭乘摩托车的路程为______千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
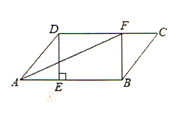
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°.
(1)若a:b=3:4,c=10,则a=_______,b=_______;
(2)若a=6,b=8,则斜边c上的高h=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )
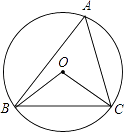
A.3
B.4
C.5
D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】把任意一个各个数位上的数字均不为0的多位自然数称为“完美数”,若将一个三位“完美数“的各数位上的数字两两组合,形成六个新的两位数,我们将这六个两位相加的和,叫做该三位“完美数”的“完美双和”,然后用所得的“完美双和”除以18,得到的结果记为
 ,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,
,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,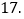 则:
则: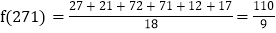
(1)填空:
 ______;
______;(2)证明:任意一个三位“完美数”的“完美双和”与该三位“完美数”各数位上数字之差能被21除;
(3)已知一个三位“完美数”
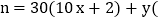 其中
其中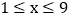 ,
,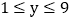 且x,均为整数
且x,均为整数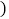 ,满足百位数字与个位数字之和等于十位数字的2倍加1,求出
,满足百位数字与个位数字之和等于十位数字的2倍加1,求出 .
.
相关试题

