【题目】计算
(1)计算:(3﹣π)0+4sin45°﹣ ![]() +|1﹣
+|1﹣ ![]() |
|
(2)化简求值:( ![]() +
+ ![]() )÷
)÷ ![]() ,其中x=6.
,其中x=6.
参考答案:
【答案】
(1)解:原式=1+4﹣2 ![]() +
+ ![]() ﹣1
﹣1
=4﹣2 ![]() +
+ ![]()
(2)解:当x=6时,
∴原式=( ![]() ﹣
﹣ ![]() )×
)× ![]()
= ![]() ﹣
﹣ ![]()
= ![]()
=﹣ ![]()
【解析】(1)根据任何一个不等于零的数的零次幂都等于1;原式=1+4﹣2![]() +
+![]() ﹣1=4﹣2
﹣1=4﹣2![]() +
+ ![]() ;(2)先把原分式的分子分母分解因式,化简为最简分式;当x=6时,原式=
;(2)先把原分式的分子分母分解因式,化简为最简分式;当x=6时,原式=![]() =-
=-![]() .
.
【考点精析】根据题目的已知条件,利用零指数幂法则和特殊角的三角函数值的相关知识可以得到问题的答案,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )
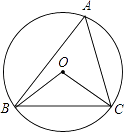
A.3
B.4
C.5
D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】把任意一个各个数位上的数字均不为0的多位自然数称为“完美数”,若将一个三位“完美数“的各数位上的数字两两组合,形成六个新的两位数,我们将这六个两位相加的和,叫做该三位“完美数”的“完美双和”,然后用所得的“完美双和”除以18,得到的结果记为
 ,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,
,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,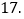 则:
则: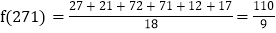
(1)填空:
 ______;
______;(2)证明:任意一个三位“完美数”的“完美双和”与该三位“完美数”各数位上数字之差能被21除;
(3)已知一个三位“完美数”
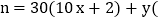 其中
其中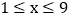 ,
,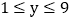 且x,均为整数
且x,均为整数 ,满足百位数字与个位数字之和等于十位数字的2倍加1,求出
,满足百位数字与个位数字之和等于十位数字的2倍加1,求出 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有2019条直线
 且有
且有 …,则直线
…,则直线 与
与 的位置关系是___________.
的位置关系是___________. -
科目: 来源: 题型:
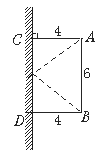
查看答案和解析>>【题目】如图,A.B两点都与平面镜相距4米,且A.B两点相距6米,一束光线由A射向平面镜反射之后恰巧经过B点.求B点到入射点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师为了解初三女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
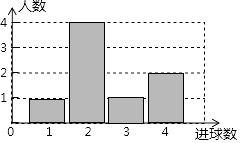
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有初三女生400人,从中任选一位女生,求选到的女生投篮成绩为“优秀”等级的概率? -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD的对角线相交于点O,AC=
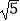 ,CD=1,
,CD=1,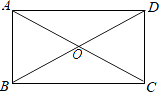
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断.
相关试题

