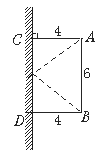
【题目】如图,A.B两点都与平面镜相距4米,且A.B两点相距6米,一束光线由A射向平面镜反射之后恰巧经过B点.求B点到入射点的距离.
参考答案:
【答案】5米
【解析】
试题作出B点关于CD的对称点B′,连结AB′,交CD于点O,则O点就是光的入射点,先根据“SSS”证得△B′DO≌△ACO,即可求得OC、OD的长,
连结OB,在Rt△ODB中,根据勾股定理即可求得结果.
作出B点关于CD的对称点B′,连结AB′,交CD于点O,则O点就是光的入射点.
因为B′D=DB.
所以B′D=AC.
∠B′DO=∠OCA=90°,
∠B′=∠CAO
所以△B′DO≌△ACO(SSS)
则OC=OD=![]() AB=
AB=![]() ×6=3米.
×6=3米.
连结OB,在Rt△ODB中,OD2+BD2=OB2
所以OB2=32+42=52,即OB=5(米).
所以点B到入射点的距离为5米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把任意一个各个数位上的数字均不为0的多位自然数称为“完美数”,若将一个三位“完美数“的各数位上的数字两两组合,形成六个新的两位数,我们将这六个两位相加的和,叫做该三位“完美数”的“完美双和”,然后用所得的“完美双和”除以18,得到的结果记为
 ,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,
,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,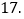 则:
则: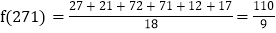
(1)填空:
 ______;
______;(2)证明:任意一个三位“完美数”的“完美双和”与该三位“完美数”各数位上数字之差能被21除;
(3)已知一个三位“完美数”
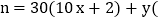 其中
其中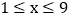 ,
,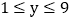 且x,均为整数
且x,均为整数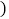 ,满足百位数字与个位数字之和等于十位数字的2倍加1,求出
,满足百位数字与个位数字之和等于十位数字的2倍加1,求出 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有2019条直线
 且有
且有 …,则直线
…,则直线 与
与 的位置关系是___________.
的位置关系是___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算:(3﹣π)0+4sin45°﹣ +|1﹣
+|1﹣  |
|
(2)化简求值:( +
+  )÷
)÷  ,其中x=6.
,其中x=6. -
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师为了解初三女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
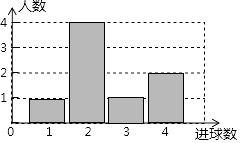
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有初三女生400人,从中任选一位女生,求选到的女生投篮成绩为“优秀”等级的概率? -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD的对角线相交于点O,AC=
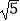 ,CD=1,
,CD=1,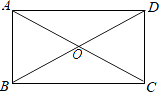
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
相关试题

