【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.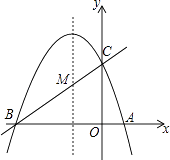
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
参考答案:
【答案】
(1)解:依题意得: 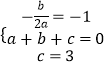 ,
,
解之得: 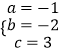 ,
,
∴抛物线解析式为y=﹣x2﹣2x+3
∵对称轴为x=﹣1,且抛物线经过A(1,0),
∴把B(﹣3,0)、C(0,3)分别代入直线y=mx+n,
得 ![]() ,
,
解之得: ![]() ,
,
∴直线y=mx+n的解析式为y=x+3;
(2)解:设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.
把x=﹣1代入直线y=x+3得,y=2,
∴M(﹣1,2),
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2);
(3)解:设P(﹣1,t),
又∵B(﹣3,0),C(0,3),
∴BC2=18,PB2=(﹣1+3)2+t2=4+t2,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,
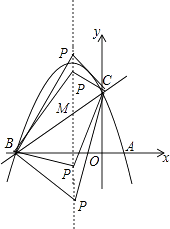
①若点B为直角顶点,则BC2+PB2=PC2即:18+4+t2=t2﹣6t+10解之得:t=﹣2;
②若点C为直角顶点,则BC2+PC2=PB2即:18+t2﹣6t+10=4+t2解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2即:4+t2+t2﹣6t+10=18解之得:t1= ![]() ,t2=
,t2= ![]() ;
;
综上所述P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1, ![]() ) 或(﹣1,
) 或(﹣1, ![]() ).
).
【解析】(1)根据对称轴为直线x=﹣1抛物线经过A(1,0),C(0,3)两点,求出函数解析式,再求出抛物线与x轴的另一个交点坐标B,将B、C两点分别代入直线y=mx+n,即可求出此函数解析式。
(2)由于点A、B关于直线x=1对称,因此设直线BC与对称轴的交点为M,则此时MA+MC的值最小,把x=﹣1代入直线y=x+3,即可求得点M的坐标。
(3)P(﹣1,t),由点B、C的坐标分别求出BC2、PB2、PC2,再分三种情况讨论:①若点B为直角顶点②若点C为直角顶点③若点P为直角顶点,建立方程,求出符合题意的t的值,即可求出点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E在AD上,以BE为折痕将△ABE翻折,点A恰好落在CD边上的点F处. 已知△EDF的周长为12,△BCF的周长为22,求CF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】早晨小欣与妈妈同时从家里出发,步行与自行车向相反方向的两地上学与上班,如图是他们离家的路程
 米
米 与时间
与时间 分钟
分钟 之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为50米
之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为50米 分钟,并且妈妈与小欣同时到达学校
分钟,并且妈妈与小欣同时到达学校 完成下列问题:
完成下列问题: 在坐标轴两处的括号内填入适当的数据;
在坐标轴两处的括号内填入适当的数据;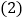 求小欣早晨上学需要的时间.
求小欣早晨上学需要的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 是最小的正整数,且
是最小的正整数,且 、
、 满足
满足 ,请回答问题:
,请回答问题:(1)请直接写出
 、
、 、
、 的值;
的值; (2)
 、
、 、
、 所对应的点分别为
所对应的点分别为 、
、 、
、 ,点
,点 为易动点,其对应的数为
为易动点,其对应的数为 ,点
,点 在
在 到
到 之间运动时(即
之间运动时(即  时),请化简式子:
时),请化简式子: (请写出化简过程);
(请写出化简过程); 
(3)在(1)(2)的条件下,点
 、
、 、
、 开始在数轴上运动,点
开始在数轴上运动,点 以每秒
以每秒 个单位长度的速度向左运动;同时,点
个单位长度的速度向左运动;同时,点 和点
和点 分别以每秒
分别以每秒 个单位长度和
个单位长度和 个单位长度的速度向右运动,假设
个单位长度的速度向右运动,假设 秒钟过后,若点
秒钟过后,若点 和点
和点 之间的距离表示为
之间的距离表示为 ,点
,点 和点
和点 之间的距离表示为
之间的距离表示为 .请问:
.请问: 的值是否随着时间
的值是否随着时间 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年中考前,张老师为了解全市初三男生体育考试项目的选择情况(每人限选一项),在全市范围内随机调查了部分初三男生,将调查结果分成五类:A.推实心球(2kg);B.立定跳远;C.半场运球;D.跳绳;E.其他,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
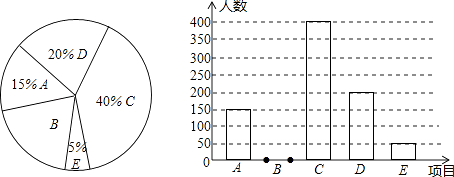
(1)将上面的条形统计图补充完整;
(2)假定全市初三毕业学生中有32000名男生,试估计全市初三男生中选半场运球的人数有多少人;
(3)甲、乙两名初三男生在上述选择率较高的三个项目:B.立定跳远;C.半场运球;D.跳绳中各选一项,同时选择半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中正确的是( )
A. +
+  =
= 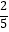
B.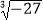 =3
=3
C.a10=(a5)2
D.b﹣2=﹣b2
相关试题

