【题目】已知,一条直线经过点A(1,3)和B(2,5).求:
(1)这个一次函数的解析式.
(2)当x=﹣3时,y的值.
(3)求此一次函数与x轴、y轴的交点坐标及其图像与两坐标轴围成的面积.
参考答案:
【答案】
(1)解:设一次函数解析式为y=kx+b,
把点A(1,3)和B(2,5)代入得 ![]() 得
得 ![]() ,
,
所以一次函数解析式为y=2x+1
(2)解:当x=﹣3时,y=2×(﹣3)+1=﹣5
(3)解:当x=0时,y=﹣1;则一次函数与y轴的交点坐标为(0,﹣1);
当y=0时,2x+1=0,解得x=﹣ ![]() ,则一次函数与x轴的交点坐标为(﹣
,则一次函数与x轴的交点坐标为(﹣ ![]() ,0);
,0);
所以该函数图像与两坐标轴所围成的三角形的面积= ![]() ×1×
×1× ![]() ×=
×= ![]()
【解析】(1)利用待定系数法求一次函数解析式;(2)把x=﹣3代入求得别的解析式,即可求得;(3)先根据坐标轴上点的坐标特征确定直线与x轴和y轴的交点坐标,然后根据三角形面积公式计算该函数图像与两坐标轴所围成的三角形的面积;
【考点精析】利用一次函数的性质和确定一次函数的表达式对题目进行判断即可得到答案,需要熟知一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[动手操作] 如图所示,地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无缝隙的地面?
(2)像上面那样铺地砖,能否全用正十边形的材料?为什么?
(3)你能不能另外想出用一种相同的正多边形材料铺地面的方案?并画出草图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),点C的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC=8 cm,BD=6cm,DH⊥AB于H,求DH的长.
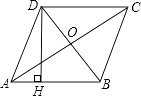
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,OE=OF.求证:△AOE≌△BOF,AE⊥BF.
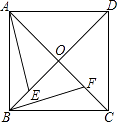
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
相关试题

