【题目】在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),点C的坐标是 . 
参考答案:
【答案】(8,4)
【解析】解:过A、C作AE⊥x轴,CF⊥x轴, 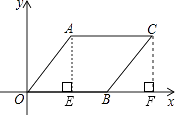
∵点A的坐标是(3,4),
∴AO=5,
∵四边形AOBC是菱形,
∴AO=AC=BO=BC=5,AO∥BC,
∴∠AOB=∠CBF,
∵AE⊥x轴,CF⊥x轴,
∴∠AEO=∠CFO=90°,
在△AOE和△CBF中 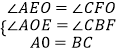 ,
,
∴△AOE≌△CBF(AAS),
∴EO=BF=3,
∵BO=5,
∴FO=8,
∴C(8,4).
所以答案是:(8,4).
【考点精析】本题主要考查了菱形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是( )

A.h≤17cm
B.h≥8cm
C.15cm≤h≤16cm
D.7cm≤h≤16cm -
科目: 来源: 题型:
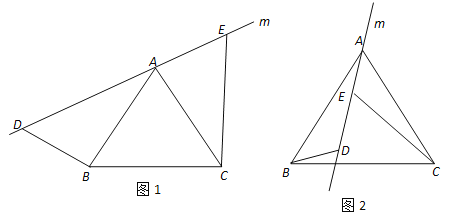
查看答案和解析>>【题目】探索与证明:(1)如图1,直线m经过正三角形ABC的顶点A,在直线m上取两点 D,E,使得∠ADB=60°,∠AEC=60°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明;
(2)将(1)中的直线m绕点A逆时针方向旋转一个角度到如图2的位置,并使∠ADB=120°,∠AEC=120°.通过观察或测量,请直接写出线段BD,CE与DE之间满足的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[动手操作] 如图所示,地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无缝隙的地面?
(2)像上面那样铺地砖,能否全用正十边形的材料?为什么?
(3)你能不能另外想出用一种相同的正多边形材料铺地面的方案?并画出草图.

-
科目: 来源: 题型:
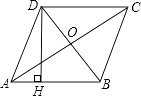
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC=8 cm,BD=6cm,DH⊥AB于H,求DH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,一条直线经过点A(1,3)和B(2,5).求:
(1)这个一次函数的解析式.
(2)当x=﹣3时,y的值.
(3)求此一次函数与x轴、y轴的交点坐标及其图像与两坐标轴围成的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.

相关试题

