【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.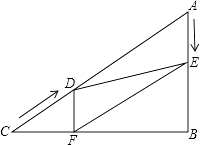
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
参考答案:
【答案】
(1)
证明:∵直角△ABC中,∠C=90°﹣∠A=30°.
∵CD=4t,AE=2t,
又∵在直角△CDF中,∠C=30°,
∴DF= ![]() CD=2t,
CD=2t,
∴DF=AE;
(2)
解:∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60﹣4t=2t,
解得:t=10,
即当t=10时,AEFD是菱形;
(3)
解:当t= ![]() 时△DEF是直角三角形(∠EDF=90°);
时△DEF是直角三角形(∠EDF=90°);
当t=12时,△DEF是直角三角形(∠DEF=90°).理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4t,
∴DF=2t=AE,
∴AD=4t,
∴4t+4t=60,
∴t= ![]() 时,∠EDF=90°.
时,∠EDF=90°.
当∠DEF=90°时,DE⊥EF,
∵四边形AEFD是平行四边形,
∴AD∥EF,
∴DE⊥AD,
∴△ADE是直角三角形,∠ADE=90°,
∵∠A=60°,
∴∠DEA=30°,
∴AD= ![]() AE,
AE,
AD=AC﹣CD=60﹣4t,AE=DF= ![]() CD=2t,
CD=2t,
∴60﹣4t=t,
解得t=12.
综上所述,当t= ![]() 时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).
时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).
【解析】(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;(3)分两种情况讨论即可求解.
【考点精析】关于本题考查的菱形的性质和解直角三角形,需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB为锐角,如图(1).
(1)若OM平分∠AOC,ON平分∠BOD,∠MON=32°,∠COD=10°,如图(2)所示,求∠AOB的度数.
(2)若OM,OD,OC,ON是∠AOB的五等分线,如图(3)所示,以射线OA,OM,OD,OC,ON,OB为始边的所有角的和为980°,求∠AOB的度数.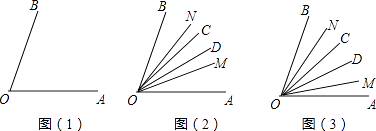
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AD⊥BC于点D,且BD=CD,若AB=3,则AC=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a3÷a2的结果是( )
A.a5 B.a-1 C.a D.a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,AB=3,BC=4,则□ABCD的周长等于_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,以a、b、c为边长的三角形不是直角三角形的是( )
A.a=3,b=4,c=5
B.a=5,b=12,c=13
C.a=1,b=2,c=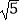
D.a= ,b=2,c=3
,b=2,c=3 -
科目: 来源: 题型:
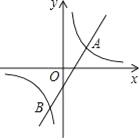
查看答案和解析>>【题目】如图,反比例函数
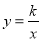 (k≠0)图象经过点(1,2),并与直线y=2x+b交于点A(x1,y1),B(x2,y2),且满足(x1+x2)(1﹣x1x2)=3.
(k≠0)图象经过点(1,2),并与直线y=2x+b交于点A(x1,y1),B(x2,y2),且满足(x1+x2)(1﹣x1x2)=3.(1)求k的值;
(2)求b的值及点A,B的坐标.
相关试题

