【题目】已知∠AOB为锐角,如图(1).
(1)若OM平分∠AOC,ON平分∠BOD,∠MON=32°,∠COD=10°,如图(2)所示,求∠AOB的度数.
(2)若OM,OD,OC,ON是∠AOB的五等分线,如图(3)所示,以射线OA,OM,OD,OC,ON,OB为始边的所有角的和为980°,求∠AOB的度数. 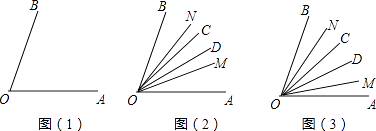
参考答案:
【答案】
(1)解:∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=∠COM,
同理:∠BON=∠DON,
∵∠MON=32°,∠COD=10°,∠MON=∠CON+∠DON﹣∠COD,
∴32°=∠COM+∠DON﹣10°,
∴∠COM+∠DON=42°,
∴∠AOM+∠BON=42°,
∵∠AOB=∠AOM+∠BON+∠MON,
∴∠AOB=42°+32°=74°
(2)解:设∠AOB被五等分的每个角为x°,则∠AOB=5x°,
以射线OA为始边的所有角的度数为x°+2x°+3x°+4x°+5x°=15x°,
以射线OM,OD,OC,ON,OB为始边的所有角的度数分别为11x°,9x°,9x°11x°,15x°,
由题意得15x+11x+9x+9x+11x+15x=980,
解得x=14.
故∠AOB=5×14°=70°
【解析】(1)根据角平分线的定义容易得到,∠MON=∠CON+∠DON﹣∠COD,根据已知条件求得∠COM+∠DON=42°,即可求得∠AOM+∠BON=42°,从而求得∠AOB=∠AOM+∠BON+∠MON=74.(2)设∠AOB被五等分的每个角为x°,则∠AOB=5x°,分别表示出以射线OA、OM、OD、OC、ON、OB为始边的所有角的度数,根据题意列出关于x的方程,解方程求得x的值,即可求得∠AOB的度数.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角的运算的理解,了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是一个菱形绿地,其周长为40
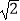 m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2 , 请问需投资金多少元?(结果保留整数)
m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2 , 请问需投资金多少元?(结果保留整数) 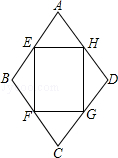
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
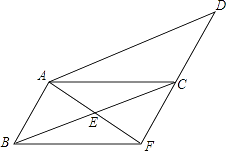
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】截止2013年底,中国高速铁路营运里程达到11000km,居世界首位,将11000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AD⊥BC于点D,且BD=CD,若AB=3,则AC=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a3÷a2的结果是( )
A.a5 B.a-1 C.a D.a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
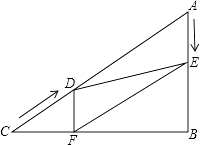
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
相关试题

