【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮? 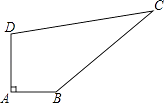
参考答案:
【答案】解:连接BD, 在Rt△ABD中,BD2=AB2+AD2=32+42=52 ,
在△CBD中,CD2=132 , BC2=122 ,
而122+52=132 ,
即BC2+BD2=CD2 ,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC= ![]() ADAB+
ADAB+ ![]() DBBC,
DBBC,
= ![]() ×4×3+
×4×3+ ![]() ×12×5=36.
×12×5=36.
所以需费用36×200=7200(元).
【解析】仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.
【考点精析】通过灵活运用勾股定理的概念和勾股定理的逆定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一边的夹角为80°,则顶角的度数为 .
-
科目: 来源: 题型:
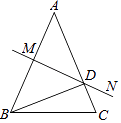
查看答案和解析>>【题目】如图,已知AB=AC,∠A=40°,AB=10,DC=3,AB的垂直平分线MN交AC于点D,则∠DBC=度,BD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(π﹣3.14)0+|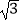 ﹣2|﹣
﹣2|﹣  +(
+(  )﹣2 .
)﹣2 .
(2)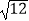 ﹣4
﹣4 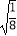 ﹣(
﹣( 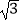 ﹣
﹣ 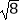 ).
).
(3)(x﹣3)(3﹣x)﹣(x﹣2)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,采用的调查方式不适宜的是( )
A. 了解我市中学生的节水意识采取抽样调查的方式
B. 为了调查一个省的环境污染情况,调查该省的省会城市
C. 了解观众对一部电影的评价情况,调查座号为奇数号的现众
D. 了解飞行员视力的达标率采取普查方式
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别是4,8,则它的周长为( )
A. 12 B. 16 C. 20 D. 16或20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
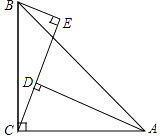
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
相关试题

