【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 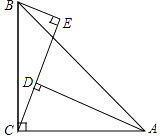
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
参考答案:
【答案】
(1)证明:如图,∵AD⊥CE,∠ACB=90°,
∴∠ADC=∠ACB=90°,
∴∠BCE=∠CAD(同角的余角相等).
在△ADC与△CEB中,
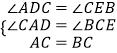 ,
,
∴△ADC≌△CEB(AAS)
(2)解:由(1)知,△ADC≌△CEB,则AD=CE=5cm,CD=BE.
如图,∵CD=CE﹣DE,
∴BE=AD﹣DE=5﹣3=2(cm),即BE的长度是2cm
【解析】(1)根据全等三角形的判定定理AAS推知:△ADC≌△CEB;(2)利用(1)中的全等三角形的对应边相等得到:AD=CE=5cm,CD=BE.则根据图中相关线段的和差关系得到BE=AD﹣DE.
-
科目: 来源: 题型:
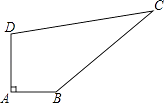
查看答案和解析>>【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,采用的调查方式不适宜的是( )
A. 了解我市中学生的节水意识采取抽样调查的方式
B. 为了调查一个省的环境污染情况,调查该省的省会城市
C. 了解观众对一部电影的评价情况,调查座号为奇数号的现众
D. 了解飞行员视力的达标率采取普查方式
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别是4,8,则它的周长为( )
A. 12 B. 16 C. 20 D. 16或20
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)2x3-4x2+2x;
(2)(m-n)(3m+n)2+(m+3n)2(n-m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“在山区建设公路时,时常要打通一条隧道,就能缩短路程”,其中蕴含的数学道理是( )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 过一点,有无数条直线 D. 连接两点之间的线段的长度是两点间的距离
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
相关试题

