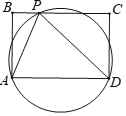
【题目】在矩形ABCD中,AB=4,BC=6,动点P为矩形边上的一点,点P沿着B﹣C的路径运动(含点B和点C),则△ADP的外接圆的圆心O的运动路径长是_____.
参考答案:
【答案】![]()
【解析】分析:如图,连接AC、BD交于点O′.当点P与B或C重合时,△PAD的外接圆的圆心与O′重合,当PA=PD时,设△PAD的外接圆的圆心为O,PO的延长线交AD于E,设PO=OD=x,因为△PAD的外心在线段AD的垂直平分线上,
观察图象可知,点P沿着B-C的路径运动,△ADP的外接圆的圆心O的运动路径长是2OO′,由此即可解决问题;
详解:如图,连接AC、BD交于点O′.
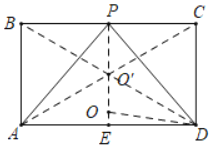
当点P与B或C重合时,△PAD的外接圆的圆心与O′重合,
当PA=PD时,设△PAD的外接圆的圆心为O,PO的延长线交AD于E,设PO=OD=x,
Rt△ODE中,∵OD2=OE2+DE2,
∴x2=(4-x)2+32,
解得x=![]() ,
,
∴OE=4-![]() =
=![]() ,
,
∵O′B=O′D,AE=DE,
∴O′E=![]() AB=2,
AB=2,
∴OO′=O′E-OE=![]() ,
,
∵△PAD的外心在线段AD的垂直平分线上,
观察图象可知,点P沿着B-C的路径运动,△ADP的外接圆的圆心O的运动路径长是2OO′=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;②△HED的面积是1﹣
 ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG= .其中正确的结论是( )
.其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数
 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

-
科目: 来源: 题型:
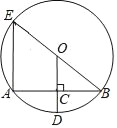
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连接BO并延长交⊙O于点E,连接AE,若AB=6,CD=1,则AE的长为( )
A. 3
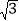 B. 8 C. 12 D. 8
B. 8 C. 12 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地图书馆为了满足群众多样化阅读的需求,决定购买甲、乙两种品牌的电脑若干组建电子阅览室.经了解,甲、乙两种品牌的电脑单价分别3100元和4600元.
(1)若购买甲、乙两种品牌的电脑共50台,恰好支出200000元,求甲、乙两种品牌的电脑各购买了多少台?
(2)若购买甲、乙两种品牌的电脑共50台,每种品牌至少购买一台,且支出不超过160000元,共有几种购买方案?并说明哪种方案最省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是⊙O直径CA的延长线上一点,点B在⊙O上,且AB=AD=AO.
(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,弦AE与BC相交于点F,且CF=9,cos∠BFA=
 ,求EF的长.
,求EF的长.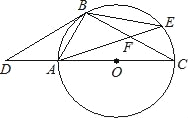
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
相关试题

