Question

【题目】如图，直线与x轴交于点A，与y轴交于B，点P是x轴上的一个动点.
（1）求A、B两点的坐标；

（2）当点P在x轴正半轴上，且△APB的面积为8时，求直线PB的解析式；

（3）点Q在第二象限，是否存在以A、B、P、Q为顶点的四边形是菱形？若存在，请求出点Q的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）B(0,4),A（﹣3，0）；（2）y=﹣x+4；（3）（﹣5，4）或（﹣，4）

【解析】

（1）根据坐标轴上点的特点即可得出结论；
（2）设出点P坐标，利用△PAB的面积建立方程求出P的坐标，最后用待定系数法求解即可；
（3）先判断出点Q在直线y=4上，再分两种情况讨论计算即可．

（1）令x=0时，y=4， ∴B（0，4），

令y=0时， x+4=0，

∴x=﹣3，

∴A（﹣3，0）；

（2）设点P（m，0）（m＞0）， ∵A（﹣3，0），

∴AP=m﹣（﹣3）=m+3，

∵△APB的面积为8，

∴S△APB= AP×OB= （m+3）×4=8，

∴m=1，

∴P（1，0），

∵B（0，4），

∴设直线PB的解析式为y=kx+4，

∴k+4=0，

∴k=﹣4，

∴直线PB的解析式为y=﹣x+4；

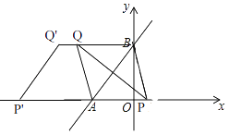
（3）如图，

∵以A、B、P、Q为顶点的四边形是菱形，且P在x轴上，

∴BQ∥AP，

∴点Q在直线y=4上，

由（1）知，A（﹣3，0），B（0，4），

∴AB=5，

∵点Q在第二象限内，

∴①当AB为菱形的边时，

∴BQ'=AB=5，

∴Q'（﹣5，4），

②当AB为菱形的对角线时，AB，PQ互相垂直平分，

∵直线AB的解析式为y= x+4，

∴直线PQ的解析式为y=﹣ x+ ，

当y=4时，则﹣ x+ =4，

∴x=﹣ ，

∴Q（﹣ ，4），

∴满足条件的点Q的坐标为（﹣5，4）或（﹣ ，4）．