【题目】某校七年级2班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):

(l)甲队成绩的中位数是____分,乙队成绩的众数是____分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队的平均成绩是9分,方差是1.4分,则成绩较为整齐的是哪个队?
参考答案:
【答案】(1)9.5,10;(2)![]() ,
,![]() ;(3)乙对成绩较为整齐.
;(3)乙对成绩较为整齐.
【解析】
(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
解::(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),则中位数是9.5分;乙队成绩中10出现了4次,出现的次数最多,则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)![]() ,
,
![]() ,
,
(3)因为甲、乙两队的平均分相同,![]() ,
,
所以乙对成绩较为整齐.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数。
例如,
 展开式中的系数1、2、1恰好对应图中第三行的数字;
展开式中的系数1、2、1恰好对应图中第三行的数字;再如,
 展开式中的系数1、3、3、1恰好对应图中第四行的数字。
展开式中的系数1、3、3、1恰好对应图中第四行的数字。请认真观察此图,写出(a+b)4的展开式,(a+b)4=_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为
 ,点
,点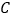 在圆周上(异于
在圆周上(异于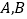 ),
),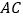 是
是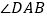 的平分线,
的平分线,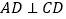 .
.(1)求证:直线
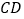 是⊙O的切线;
是⊙O的切线;(2)若
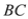 =3,
=3,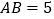 ,求
,求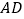 的值.
的值.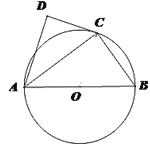
-
科目: 来源: 题型:
查看答案和解析>>【题目】一方有难八方支援,某市政府筹集抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车来运送,需运费8200元,则分别需甲、乙两种车各几辆?
(2)为了节约运费,该市政府共调用16辆甲、乙,丙三种车都参与运送物资,试求出有几种运送方案,哪种方案的运费最省?其费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】O为直线AB上的一点,OC⊥OD,射线OE平分∠AOD.

(1)如图①,判断∠COE和∠BOD之间的数量关系,并说明理由;
(2)若将∠COD绕点O旋转至图②的位置,试问(1)中∠COE和∠BOD之间的数量关系是否发生变化?并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,探究∠COE和∠BOD之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
(1)求A、B两点的坐标;(2)当点P在x轴正半轴上,且△APB的面积为8时,求直线PB的解析式;
(3)点Q在第二象限,是否存在以A、B、P、Q为顶点的四边形是菱形?若存在,请求出点Q的坐标,若不存在,请说明理由.

相关试题

