【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
参考答案:
【答案】C
【解析】
试题甲的作法正确:
∵四边形ABCD是平行四边形,∴AD∥BC。∴∠DAC=∠ACN。
∵MN是AC的垂直平分线,∴AO=CO。
在△AOM和△CON中,∵∠MAO=∠NCO,AO=CO,∠AOM=∠CON,
∴△AOM≌△CON(ASA),∴MO=NO。∴四边形ANCM是平行四边形。
∵AC⊥MN,∴四边形ANCM是菱形。
乙的作法正确:如图,
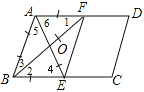
∵AD∥BC,∴∠1=∠2,∠6=∠4。
∵BF平分∠ABC,AE平分∠BAD,∴∠2=∠3,∠5=∠6。
∴∠1=∠3,∠5=∠4。∴AB=AF,AB=BE。∴AF=BE。
∵AF∥BE,且AF=BE,∴四边形ABEF是平行四边形。
∵AB=AF,∴平行四边形ABEF是菱形。
故选C。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
与x轴交于点A,与y轴交于B,点P是x轴上的一个动点.
(1)求A、B两点的坐标;(2)当点P在x轴正半轴上,且△APB的面积为8时,求直线PB的解析式;
(3)点Q在第二象限,是否存在以A、B、P、Q为顶点的四边形是菱形?若存在,请求出点Q的坐标,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数
 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出
 的x的取值范围;
的x的取值范围;(3)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,俄罗斯方块游戏中,图形
 经过平移使其填补空位,则正确的平移方式是( )
经过平移使其填补空位,则正确的平移方式是( )[Failed to download image : http://192.168.0.10:8086/QBM/2019/8/9/2265110730670080/2266396395864065/STEM/34cd169bb880437797498d7a59a34864.png]
A.先向右平移5格,再向下平移3格
B.先向右平移4格,再向下平移5格
C.先向右平移4格,再向下平移4格
D.先向右平移3格,再向下平移5格
-
科目: 来源: 题型:
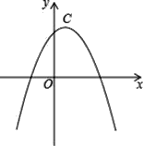
查看答案和解析>>【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:
零花钱数额
 元
元人数(频数)
频率

6
0.15

12
0.30

16
0.40


0.10

2


请根据以下图表,解答下列问题:
(1)这次被调查的人数共有__________人,
 __________;
__________;(2)计算并补全频数分布直方图;
(3)请估计该校1500名学生中每月零花钱数额低于90的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请从以下四个一元二次方程中任选三个,并用适当的方法解这三个方程.
(1)x2﹣x﹣1=0;
(2)(y﹣2)2﹣12=0;
(3)(1+m)2=m+1;
(4)t2﹣4t=5.
相关试题

