【题目】如图,长方形ABCD中,AB=8,BC=12,点E是边BC上一点,BE=5,点F是射线BA上一动点,连接EF,将△BEF沿着EF折叠,使B点的对应点P落在长方形一边的垂直平分线上,连接BP,则BP的长是_____.

参考答案:
【答案】4![]() 或
或![]() 或2
或2![]()
【解析】
分三种情况:①当P落在AB边的垂直平分线上且F在BA的延长线上时;②当P落在AB边的垂直平分线上且F在BA上时;③当P落在BC边的垂直平分线上时;由折叠的性质和勾股定理即可得出答案.
解:分三种情况:①当P落在AB边的垂直平分线上时,如图1所示:
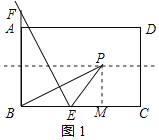
作PM⊥BC于M,则PM=![]() AB=4,∠PMB=90°,
AB=4,∠PMB=90°,
由折叠的性质得:PE=BE=5,
∴EM=![]() =3,
=3,
∴BM=BE+EM=8,
∴BP=![]() ;
;
②当P落在AB边的垂直平分线上,且F在线段BA上时,如图2所示:
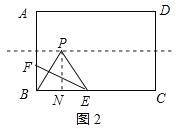
作PN⊥BC于N,则PN=![]() AB=4,∠PNB=90°,
AB=4,∠PNB=90°,
由折叠的性质得:PE=BE=5,
∴EN=![]() =3,
=3,
∴BN=BE-EN=2,
∴BP=![]() ;
;
③当P落在BC边的垂直平分线上时,如图3所示:
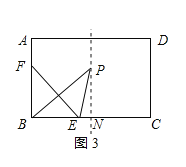
则BN=![]() BC=6,∠PNB=90°,
BC=6,∠PNB=90°,
由折叠的性质得:PE=BE=5,
∴EN=BN-BE=1,PN=![]() ,
,
∴BP=![]() ;
;
综上所述,BP的长是4![]() 或
或![]() 或2
或2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1面积为S1,△B3D2C2面积为S2,…,△Bn+1DnCn面积为Sn,则Sn等于( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口B和点落水点C在同一直线上,洗手盆及水龙头的相关数据如图2.(参考数据:sin37°=
 ,cos37°=
,cos37°= ,tan37°=
,tan37°= )
)求把手端点A到BD的距离;
求CH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?

-
科目: 来源: 题型:
查看答案和解析>>【题目】数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以互相转化.树形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.
(1) (思想应用)已知m, n均为正实数,且m+n=2求
 的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.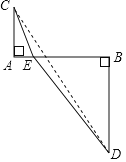
①用含m的代数式表示CE=_______, 用含n的代数式表示DE= ;
②据此求
 的最小值;
的最小值;(2)(类比应用)根据上述的方法,求代数式
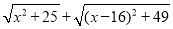 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形例如:某三角形三边长分别是5,6和8,因为
 ,所以这个三角形是常态三角形.
,所以这个三角形是常态三角形.
(1)若△ABC三边长分别是2,
 和4,则此三角形 常态三角形(填“是”或“不是”);
和4,则此三角形 常态三角形(填“是”或“不是”);(2)如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,CD=
 AB, 若△ACD是常态三角形,求△ABC的面积;,
AB, 若△ACD是常态三角形,求△ABC的面积;,(3)若Rt△ABC是常态△,斜边是
 ,则此三角形的两直角边的和= .
,则此三角形的两直角边的和= .
相关试题

