【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于点F,连接CF。
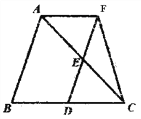
(1)求证:四边形ABDF是平行四边形;
(2)若∠CAF=45°,BC=4,CF=![]() ,求AB的长。
,求AB的长。
参考答案:
【答案】(1)证明见解析;
(2)AB的长为![]()
【解析】分析:(1)求出DE∥AB,AF∥BC来证明四边形ABDF是平行四边形.
(2)过点F作FG⊥AC于G点,求出AC和GF的长再求△CAF的面积.
本题解析:
证明:(1)在△ABC中,点D、E分别是边BC、AC的中点,
∴DE∥AB, 又知AF∥BC,∴四边形ABDF是平行四边形。
(2)过点F作FG交AC于点G,过点A作AH交BC于点H。
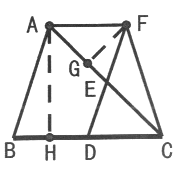
∵FG⊥AC,∴∠AGF=90°,∵∠CAF=45°,由(1)知,四边形ABDF是平行四边形,
∴AF=BD=![]() BC=2,在RT△AFG中,∠CAF=45°,∴AG=GF=
BC=2,在RT△AFG中,∠CAF=45°,∴AG=GF=![]() AF=
AF=![]() 。在RT△CFG中,CF=
。在RT△CFG中,CF=![]() ,
,
∴CG=![]() ,∵AF∥BC,∴∠ACB=45°,
,∵AF∥BC,∴∠ACB=45°,
∵AH⊥BC,在RT△ACH中,AC=AG+GC=![]() +2
+2![]() =3
=3![]() ,∴AH=HC=
,∴AH=HC=![]() ×3
×3![]() =3,
=3,
∴BH=BC-CH=4-3=1。在RT△ABH中,AB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣3
﹣

﹣2
﹣1
0
1
2

3
…
y
…
3
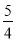
m
﹣1
0
﹣1
0

3
…
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中是必然事件的是( )
A.小婷上学一定坐公交车
B.买一张电影票,座位号正好是偶数
C.小红期末考试数学成绩一定得满分
D.将豆油滴入水中,豆油会浮在水面上
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级一班在召开期末总结表彰会前,班主任安排班长李小波去商店买奖品,下面是李小波与售货员的对话:
李小波:阿姨,您好!
售货员:同学,你好,想买点什么?
李小波:我只有100元,请帮我安排买10支钢笔和15本笔记本.
售货员:好,每支钢笔比每本笔记本贵2元,退你5元,请清点好,再见.
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD和平行四边形AECF的顶点,D,E,F,B在一条直线上,则下列等式成立的是( )
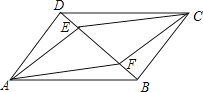
A.AE=CE
B.CE=CF
C.DE=BF
D.DE=EF=BF -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行摸牌游戏。现有四张形状大小完全相同的牌,正面分别标有数字1,2,3,4。将四张牌背面朝上,洗匀后放在桌子上。甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张。
(1)请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字差的绝对值等于1,则甲获胜;若抽取的数字差的绝对值大于1,则乙获胜。这个游戏公平吗?请用概率的知识加以解释。
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2=4的解是( )
A.x=2B.x=﹣2C.x=±2D.没有实数根
相关试题

