【题目】问题提出
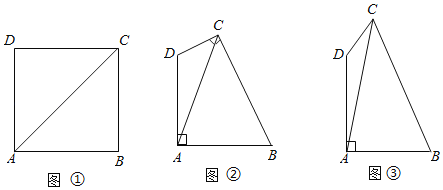
(1)如图①,在正方形ABCD中,对角线AC=8,则正方形ABCD的面积为 ;
问题探究
(2)如图②,在四边形ABCD中,AD=AB,∠DAB=∠DCB=90°,∠ADC+∠ABC=180°,若四边形ABCD的面积为8,求对角线AC的长;
问题解决
(3)如图③,四边形ABCD是张叔叔要准备开发的菜地示意图,其中边AD和AB是准备用砖来砌的砖墙,且满足AD=AB,∠DAB=90°,边DC和CB是准备用现有的长度分别为3米和7米的竹篱笆来围成的篱笆墙,即DC=3米,CB=7米.按照这样的想法,张叔叔围成的菜园里对角线AC的长是否存在最大值呢?若存在,求出这个最大值;若不存在,说明理由.
参考答案:
【答案】(1)32;(2)4;(3)存在,最大值为5![]() .
.
【解析】
(1)先根据勾股定理求出AB的长,然后再根据面积公式解答即可;
(2)先说明△ADC'≌△ABC(SAS),进而得出S△ADC'=S△ABC,AC'=AC,然后再根据面积公式解答即可;
(3先判断出点D在CC'上时, AC最大,求出AC的长即可.
解:(1)∵AC是正方形的对角线,
∴∠B=90°,AB=BC,
在Rt△ABC中,AC=8,
根据勾股定理得,AB2+BC2=AC2,
∴2AB2=AC2=64,
∴AB2=32,
∴S正方形ABCD=32,
故答案为32;
(2)如图②,延长CD至C'使DC'=BC,连接AC',
∴∠ADC+∠ADC'=180°,
∵∠ADC+∠ABC=180°,
∴∠ADC'=∠ABC,
∵AD=AB,
∴△ADC'≌△ABC(SAS),
∴S△ADC′=S△ABC,AC'=AC,
∴∠DAC'=∠BAC,
∴∠DAC'+∠CAD=∠BAC+∠CAD=∠BAD=90°,
∴∠CAC'=90°,
∵S四边形ABCD=S△ABC+S△ADC=S△ADC′+S△ADC=S△ACC′=8,
∵S△ACC′=![]() ACAC'=
ACAC'=![]() AC2=8,
AC2=8,
∴AC=4,
即AC的长为4;
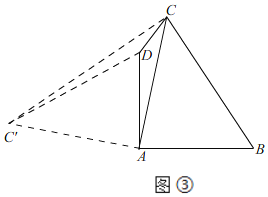
(3)如图③,
将△ABC绕点A逆时针旋转90°得△ADC',连接AC',CC',
由旋转知,AC'=AC,C'D=BC,∠CAC'=90°,
当点D在CC'上时,AC最大
此时,CC'=CD+C'D=CD+BC=10,
∴AC2=![]() CC'2=50,
CC'2=50,
∴AC=5![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“西成高铁”的开通,对于加强关中一天水经济区与成渝经济区的交流合作,促进区域经济发展和提高人民出行质量,具有十分重要的意义.成都某单位组织优秀员工利用周末乘坐“西成高铁”到西安观光旅游,计划游览着名景点“大唐芙蓉园”.已知该景区团体票价格设置如下:
人数/人
10人以内(含10人)
超过10人但不超过30人的部分
超过30人的部分
单价(元/张)
120
100
90
(1)求团体票总费用y(元)与游览人数x(人)之间的关系式;
(2)若该单位购买团体票共花费4100元,且所有人都购买了门票,那么该单位共有多少人游览了“大唐芙蓉园”?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
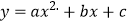 ,自变量x与函数y的对应值如下表:
,自变量x与函数y的对应值如下表:x
…
-5
-4
-3
-2
-1
0
…
y
…
4
0
-2
-2
0
4
…
下列说法正确的是( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴x=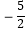
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=35°,将△ABC绕点C逆时针旋转α角到△A1B1C的位置,A1B1恰好经过点B,则旋转角α的度数等( )

A.35°
B.55°
C.65°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象如图所示,则当函数
的图象如图所示,则当函数 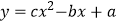 的图象在x轴上方时,x的取值范围为( )
的图象在x轴上方时,x的取值范围为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列两则材料,回答问题,材料一:定义直线y=ax+b与直线y=bx+a互为“共同体直线”,例如,直线y=x+4与直线y=4x+l互为“共同体直线”.
材料二:对于半面直角坐标系中的任意两点P1(x1,y1)、P2(x2,y2),P1、P2之两点间的直角距离d1(P1,p2)=|x1﹣x2|+|y1﹣y2|:例如:Q1(﹣3,1)、Q2(2.4)两点间的直角距离为d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8; P0(x0,y0)为一个定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做Po到直线y=ax+b的直角距离.
(1)计算S(﹣2,6),T(1,3)两点间的直角距离d(S,T)= ,直线y=4x+3上的一点H(a,b)又是它的“共同体直线”上的点,求点H的坐标.
(2)对于直线y=ax+b上的任意一点M(m,n),都有点N(3m,2m﹣3n)在它的“共同体直线”上,试求点L(10,﹣
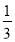 )到直线y=ax+b的直角距离.
)到直线y=ax+b的直角距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列条件中,能判断直线L1∥L2的是( )

A. ∠2=∠3 B. ∠l=∠3 C. ∠4+∠5=180
 D. ∠2=∠4
D. ∠2=∠4
相关试题

