【题目】随着“西成高铁”的开通,对于加强关中一天水经济区与成渝经济区的交流合作,促进区域经济发展和提高人民出行质量,具有十分重要的意义.成都某单位组织优秀员工利用周末乘坐“西成高铁”到西安观光旅游,计划游览着名景点“大唐芙蓉园”.已知该景区团体票价格设置如下:
人数/人 | 10人以内(含10人) | 超过10人但不超过30人的部分 | 超过30人的部分 |
单价(元/张) | 120 | 100 | 90 |
(1)求团体票总费用y(元)与游览人数x(人)之间的关系式;
(2)若该单位购买团体票共花费4100元,且所有人都购买了门票,那么该单位共有多少人游览了“大唐芙蓉园”?
参考答案:
【答案】(1)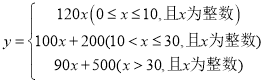 ;(2)该单位共有40人游览了“大唐芙蓉园”
;(2)该单位共有40人游览了“大唐芙蓉园”
【解析】
(1)根据表格中的数据和题意可以写出团体票价y与游览人数x之间的函数关系式;
(2)根据题意和(1)中的函数解析式可以求得该单位共有多少人游览了“大唐芙蓉园”.
解:(1)当0≤x≤10时,y=120x;
当10<x≤30时,y=120×10+100(x﹣10)=100x+200;
当x>30时,y=120×10+20×100+90(x﹣30)=90x+500;
综上, 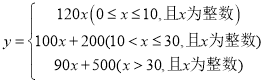 ;
;
(2)当x=30时,
y=100x+200=100×30+200=3200<4100,
∴人数x>30,
则90x+500=4100,
解得x=40,
答:该单位共有40人游览了“大唐芙蓉园”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的四个转盘中,转盘3,4被分成8等分,若让转盘自由转动一次停止后,指针落在阴影区域内可能性从大到小排列为( )

A.①②④③
B.③②④①
C.③④②①
D.④③②① -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为庆祝国庆节举办游园活动,小军来到摸球兑奖活动场地,李老师对小军说:“这里有甲、乙两个盒子,里面都装有一些乒乓球,你只能选择在其中一个盒子中摸球。”获奖规则如下:
甲盒中有白色乒乓球4个,黄色乒乓球1个,一人只能摸一次且一次摸出一个球,若这个球为黄色球,则可获得玩具熊一个,否则不得奖;
乙盒中有白色乒乓球2个,黄色乒乓球3个,一人只能摸一次且一次摸出两个球,若这两个球均为黄色球,则可获得玩具熊一个,否则不得奖;
请问小军在哪个盒子内摸球获得玩具熊的机会更大?请用概率知识说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠B=45°,过点C作CE⊥AD于点,连结AC,过点D作DF⊥AC于点F,交CE于点G,连结EF.
(1)若DG=8,求对角线AC的长;
(2)求证:AF+FG=
 EF.
EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
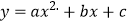 ,自变量x与函数y的对应值如下表:
,自变量x与函数y的对应值如下表:x
…
-5
-4
-3
-2
-1
0
…
y
…
4
0
-2
-2
0
4
…
下列说法正确的是( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴x=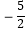
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=35°,将△ABC绕点C逆时针旋转α角到△A1B1C的位置,A1B1恰好经过点B,则旋转角α的度数等( )

A.35°
B.55°
C.65°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
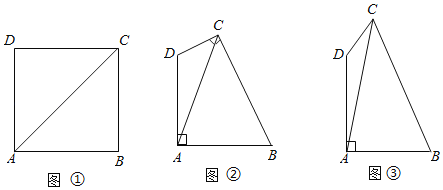
(1)如图①,在正方形ABCD中,对角线AC=8,则正方形ABCD的面积为 ;
问题探究
(2)如图②,在四边形ABCD中,AD=AB,∠DAB=∠DCB=90°,∠ADC+∠ABC=180°,若四边形ABCD的面积为8,求对角线AC的长;
问题解决
(3)如图③,四边形ABCD是张叔叔要准备开发的菜地示意图,其中边AD和AB是准备用砖来砌的砖墙,且满足AD=AB,∠DAB=90°,边DC和CB是准备用现有的长度分别为3米和7米的竹篱笆来围成的篱笆墙,即DC=3米,CB=7米.按照这样的想法,张叔叔围成的菜园里对角线AC的长是否存在最大值呢?若存在,求出这个最大值;若不存在,说明理由.
相关试题

