【题目】如图,已知直线l:y=﹣ ![]() x+3分别与x、y轴交于点A和B.
x+3分别与x、y轴交于点A和B.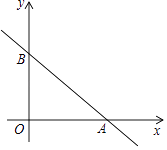
(1)求△AOB的面积;
(2)求原点O到直线l的距离.
参考答案:
【答案】
(1)解:当x=0时,y=﹣ ![]() x+3=3,
x+3=3,
∴点B的坐标为(0,3);
当y=﹣ ![]() x+3=0时,x=4,
x+3=0时,x=4,
∴点A的坐标为(4,0),
∴OA=4,OB=3,
∴S△AOB= ![]() OAOB=
OAOB= ![]() ×4×3=6
×4×3=6
(2)解:设原点O到直线l的距离为h.
在Rt△AOB中,OA=4,OB=3,∠AOB=90°,
∴AB= ![]() =5.
=5.
由面积法可得:h= ![]() =
= ![]() .
.
∴原点O到直线l的距离为 ![]()
【解析】(1)根据直线l的解析式利用一次函数图象上点的坐标特征可求出点A、B的坐标,再利用三角形的面积公式即可求出△AOB的面积;(2)设原点O到直线l的距离为h,在Rt△AOB中,利用勾股定理即可求出AB的长度,再根据△AOB的面积利用面积法即可求出原点O到直线l的距离.
【考点精析】掌握一次函数的性质是解答本题的根本,需要知道一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a∥b,a∥c,那么b与c的位置关系是( )
A.不一定平行
B.一定平行
C.一定不平行
D.以上都有可能 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF,
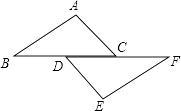
(1)求证:AB=EF.
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x4+x4=x8B.x12﹣x4=x8C.x2x4=x8D.(x2)4=x8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=0.5x+1的图象与x轴交于点A,与y轴交于点B,二次函数y=0.5x2+bx+c的图象与一次函数y=0.5x+1的图象交于点B、C两点,与x轴交于D、E两点,且D点坐标为(1,0).
(1)求二次函数的解析式;
(2)在在x轴上有一动点P,从O点出发以每秒1个单位的速度沿x轴向右运动,是否存在动点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出点P运动时间t的值;若不存在,请说明理由;
(3)若动点P在x轴上,动点Q在射线AC上,同时从A点出发,点P沿x轴正方向以每秒2个单位的速度运动,点Q以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似?若存在,求a的值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若5x﹣3y﹣2=0,则25x÷23y﹣2=_____.
相关试题

