【题目】如图,已知一次函数y=0.5x+1的图象与x轴交于点A,与y轴交于点B,二次函数y=0.5x2+bx+c的图象与一次函数y=0.5x+1的图象交于点B、C两点,与x轴交于D、E两点,且D点坐标为(1,0).
(1)求二次函数的解析式;
(2)在在x轴上有一动点P,从O点出发以每秒1个单位的速度沿x轴向右运动,是否存在动点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出点P运动时间t的值;若不存在,请说明理由;
(3)若动点P在x轴上,动点Q在射线AC上,同时从A点出发,点P沿x轴正方向以每秒2个单位的速度运动,点Q以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似?若存在,求a的值;若不存在,说明理由.

参考答案:
【答案】(1)解析式为: ![]() ;
;
(2)t=1或3;
(3)当a值为![]() 或
或![]() 时,△APQ与△ABD相似
时,△APQ与△ABD相似
【解析】试题分析:(1)根据一次函数的解析式可找出点B的坐标,再根据点A、D的坐标利用待定系数法即可求出二次函数的解析式;(2)假设存在,则点P的坐标为(t,0).联立直线与抛物线解析式成方程组,解方程组求出点C的坐标,根据点B、P的坐标利用两点间的距离公式即可求出PB、PC、BC的长度,再利用勾股定理即可得出关于t的一元二次方程,解方程即可得出结论;(3)假设存在,则AP=2t,AQ=at.由一次函数解析式即可找出点A的坐标,结合点B、D的坐标即可得出AB、AD的长度,分△PAQ∽BAD和△PAQ∽△DAB两种情况考虑,根据相似三角形的性质即可得出关于a的一元一次方程,解方程即可求出a值,此题得解.
试题解析:(1)将B(0,1),D(1,0)的坐标代入y=![]() x2+bx+c,
x2+bx+c,
得: 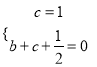 ,
,
解得: 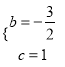 ,
,
故解析式为![]() ;
;
(2)设符合条件的点P存在,令P(a,0):
当P为直角顶点时,如图:过C作CF⊥x轴于F;
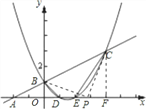
∵Rt△BOP∽Rt△PCF,
∴![]() ,
,
即![]() ,
,
整理得a24a+3=0,
解得a=1或a=3;
故可得t=1或3.
(3)存在符合条件的t值,使△APQ与△ABD相似,
①当△APQ∽△ABD时, ![]() ,
,
解得:a=![]() ;
;
②当△APQ∽△ADB时, ![]() ,
,
解得:a=![]() ,
,
∴存在符合条件的a值,使△APQ与△ABD相似,a=![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l:y=﹣
 x+3分别与x、y轴交于点A和B.
x+3分别与x、y轴交于点A和B.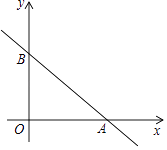
(1)求△AOB的面积;
(2)求原点O到直线l的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x4+x4=x8B.x12﹣x4=x8C.x2x4=x8D.(x2)4=x8
-
科目: 来源: 题型:
查看答案和解析>>【题目】若5x﹣3y﹣2=0,则25x÷23y﹣2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2+11x﹣12可因式分解成(x+a)(bx+c),其中a、b、c均为整数,则a+c之值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 x2﹣x﹣1=0,则 2018+2x﹣x3 的值是_____.
相关试题

