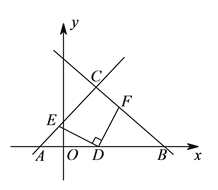
【题目】如图,在平面直角坐标系中,已知直线![]() 和
和![]() 与
与![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,设两直线相交于点
,设两直线相交于点![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上一个动点(不与点
上一个动点(不与点![]() 和
和![]() 重合),连结
重合),连结![]() ,并过点
,并过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(![]() )判断
)判断![]() 的形状,并说明理由.
的形状,并说明理由.
(![]() )当点
)当点![]() 在线段
在线段![]() 上运动时,四边形
上运动时,四边形![]() 的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
(![]() )当点
)当点![]() 的横坐标为
的横坐标为![]() 时,在
时,在![]() 轴上找到一点
轴上找到一点![]() 使得
使得![]() 的周长最小,请直接写出点
的周长最小,请直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(![]() )等腰直角三角形,理由见解析;(
)等腰直角三角形,理由见解析;(![]() )定值为8;(
)定值为8;( ![]() )
)![]()
【解析】试题分析:(1)分别求出A、B、C三点坐标以及AC、AB、BC的长,即可得出![]() 的形状;
的形状;
(2)![]() ,可知四边形
,可知四边形![]() 的面积是定值;
的面积是定值;
(3)利用轴对称的性质即可求解.
解:(![]() )由题意可知
)由题意可知![]() ,
, ![]() ,令
,令![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,且
,且![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
(![]() )由题意知
)由题意知![]() ,即
,即![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
, ![]() 于
于![]() ,
,
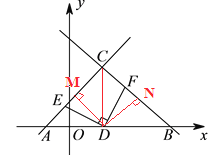
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() ,是定值.
,是定值.
(![]() )当
)当![]() 时,
时, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴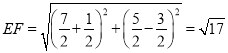 ,
,
则要使![]() 周长最小,即只需时
周长最小,即只需时![]() 最小,又两点之间线段最短,
最小,又两点之间线段最短,
∴设![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,
,
∴![]() ,令
,令![]() ,
, ![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,点
,点 点
点 分别在射线
分别在射线 ,射线
,射线 上,若点
上,若点 与点
与点 关于
关于 对称,点
对称,点 点
点 关于
关于 对称,
对称,  与
与 相交于点
相交于点 ,有以下命题:①
,有以下命题:① ;②
;② ;③若
;③若 ,
,  ;④
;④ 是等腰直角三角形,则正确的命题有( ).
是等腰直角三角形,则正确的命题有( ).
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队共同开凿一条隧道,甲队按一定的工作效率先施工,一段时间后,乙队从隧道的另一端按一定的工作效率加入施工,中途乙队遇到碎石层,工作效率降低,当乙队完成碎石层时恰好隧道被打通,此时甲队工作了
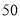 天,设甲、乙两队各自开凿隧道的长度为
天,设甲、乙两队各自开凿隧道的长度为 (米),工作时间为
(米),工作时间为 (天),
(天), 与
与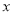 之间的函数图像如图所示,下列说法:
之间的函数图像如图所示,下列说法:①甲每天开凿隧道
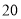 米;
米;②这条隧道总长为
 米;
米;③当乙遇上碎石层时,甲恰好开凿隧道
 米,
米,④若乙在甲施工
 天后开始施工,则乙在遇到碎石层之前的施工速度比之后快
天后开始施工,则乙在遇到碎石层之前的施工速度比之后快 米/天,其中正确的有__________.
米/天,其中正确的有__________.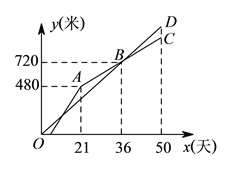
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
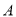 ,
,  两地相距
两地相距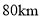 ,甲、乙两人沿同一公路从
,甲、乙两人沿同一公路从 地出发到
地出发到 地,甲骑摩托车,乙骑自行车,图中
地,甲骑摩托车,乙骑自行车,图中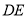 ,
,  分别表示离开
分别表示离开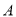 地的路程
地的路程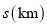 与运动时间
与运动时间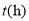 的函数关系的图像.
的函数关系的图像.(
 )写出甲、乙的速度和点
)写出甲、乙的速度和点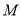 的坐标.
的坐标.(
 )若甲到达
)若甲到达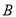 地后立刻按原速度返回至
地后立刻按原速度返回至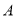 地,乙到达
地,乙到达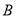 地后停止.
地后停止.①试求甲离开
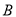 地后
地后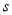 关于
关于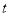 的函数表达式及自变量
的函数表达式及自变量 的取值范围,并在直角坐标系中画出它的图像.
的取值范围,并在直角坐标系中画出它的图像.②试求甲、乙两人再次相遇的时间
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一只肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同.小明喜欢吃红枣馅的粽子.
(1)请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率;
(2)在吃粽子之前,小明准备用一格均匀的正四面体骰子(如图所示)进行吃粽子的模拟试验,规定:掷得点数
 向上代表肉馅,点数
向上代表肉馅,点数 向上代表香肠馅,点数
向上代表香肠馅,点数 ,
, 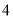 向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由.
向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由.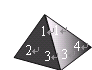
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°-7°=83°.当∠A<83°时,光线射到OB边上的点A1后,经OB反射到线段AO上的点A2,易知∠1=∠2.若A1A2⊥AO,光线又会沿A2→A1→A原路返回到点A,此时∠A=76°.…若光线从A点出发后,经若干次反射能沿原路返回到点A,则锐角∠A的最小值为______.

-
科目: 来源: 题型:
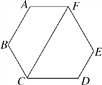
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,CF∥AB.
(1)求∠FCD的度数;
(2)求证:AF∥CD.
相关试题

