Question

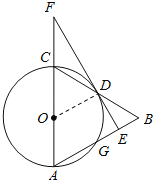
【题目】如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D是BC中点，DE⊥AB，垂足为E，交AC的延长线于点F．

（1）求证：直线EF是⊙O的切线；

（2）若CF=3，cosA=0.4，求出⊙O的半径和BE的长；

（3）连接CG，在（2）的条件下，求CG:EF的值．

Answer 1

【答案】(1)见解析；（2）2， （3）CG:EF＝4：7

【解析】试题分析：（1）连结OD．先证明OD是△ABC的中位线，根据中位线的性质得到OD∥AB，再由DE⊥AB，得出OD⊥EF，根据切线的判定即可得出直线EF是⊙O的切线；

（2）先由OD∥AB，得出∠COD=∠A，再解Rt△DOF，根据余弦函数的定义得到cos∠FOD==，设⊙O的半径为R，解方程=，求出R=，那么AB=2OD=，解Rt△AEF，根据余弦函数的定义得到cosA==，求出AE=，然后由BE=AB﹣AE即可求解．

试题解析：

（1）证明：如图，连结OD．

∵CD=DB，CO=OA，

∴OD是△ABC的中位线，

∴OD∥AB，AB=2OD，

∵DE⊥AB，

∴DE⊥OD，即OD⊥EF，

∴直线EF是⊙O的切线；

（2）解：∵OD∥AB，

∴∠COD=∠A．

在Rt△DOF中，∵∠ODF=90°，

∴cos∠FOD==，

设⊙O的半径为R，则=，

解得R=，

∴AB=2OD=．

在Rt△AEF中，∵∠AEF=90°，

∴cosA===，

∴AE=，

∴BE=AB﹣AE=﹣=2．