参考答案:
【解析】根据一元二次方程的根与系数的关系知:x1+x2=2(k+1),x1x2=k2+2,代入(x1+1)(x2+1)=8,即x1x2+(x1+x2)+1=8代入即可得到关于k的方程,可求出k的值,再根据△与0的关系舍去不合理的k值.
解:由已知定理得:x1x2=k2+2,x1+x2=2(k+1).
∴(x1+1)(x2+1)=x1x2+(x1+x2)+1=k2+2+2(k+1)+1=8.
即k2+2k-3=0,
解得:k1=-3,k2=1.
又∵△=4(k+1)2-4(k2+2)≥0.
解得:k≥![]() ,故k=-3舍去.
,故k=-3舍去.
∴k的值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AE⊥BC于点E,∠BAE=30°,AD=4cm.
(1)求菱形ABCD的各角的度数;
(2)求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一块长为a(cm),宽为b(cm)(a>b)的矩形黑板的四周,镶上宽为x(cm)的木板,得到一个新的矩形.
(1)试用含a,b,x的代数式表示新矩形的长和宽;
(2)试判断原矩形的长、宽与新矩形的长、宽是不是比例线段,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数
中位数
方差
甲
8
乙
8
2
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
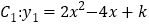 与
与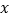 轴只有一个公共点.
轴只有一个公共点.(
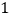 )求
)求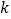 的值.
的值.(
 )怎样平移抛物线
)怎样平移抛物线 就可以得到抛物线
就可以得到抛物线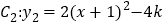 ?请写出具体的平移方法.
?请写出具体的平移方法.(
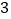 )若点
)若点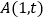 和点
和点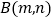 都在抛物线
都在抛物线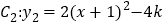 上,且
上,且 ,直接写出
,直接写出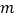 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设边长为
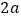 的正方形的中心
的正方形的中心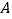 在直线
在直线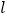 上,它的一组对边垂直于直线
上,它的一组对边垂直于直线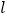 ,半径为
,半径为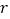 的圆的圆心
的圆的圆心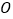 在直线
在直线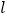 上运动,
上运动,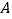 、
、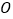 两点之间的距离为
两点之间的距离为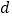 .
.(
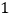 )如图①,当
)如图①,当 时,填表:
时,填表: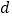 、
、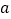 、
、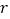 之间的数量关系
之间的数量关系⊙
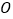 与正方形的公共点个数
与正方形的公共点个数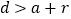
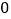
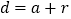
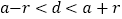
__________
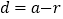
__________
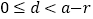
__________
(
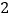 )如图②,⊙
)如图②,⊙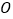 与正方形有
与正方形有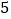 个公共点
个公共点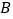 、
、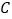 、
、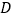 、
、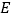 、
、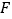 ,求此时
,求此时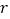 与
与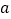 之间的数量关系:
之间的数量关系: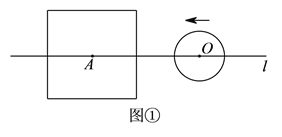

(
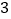 )由(
)由(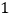 )可知,
)可知,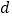 、
、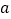 、
、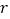 之间的数量关系和⊙
之间的数量关系和⊙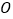 与正方形的公共点个数密切相关.当
与正方形的公共点个数密切相关.当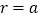 时,请根据
时,请根据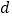 、
、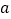 、
、 之间的数量关系,判断⊙
之间的数量关系,判断⊙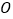 与正方形的公共点个数.
与正方形的公共点个数.(
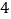 )当
)当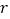 与
与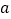 之间满足(
之间满足(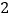 )中的数量关系时,⊙
)中的数量关系时,⊙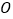 与正方形的公共点个数为__________.
与正方形的公共点个数为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
如图
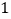 ,在平面直角坐标系
,在平面直角坐标系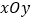 中,直线
中,直线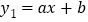 与双曲线
与双曲线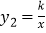 交于
交于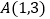 和
和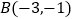 两点.
两点.观察图象可知:①当
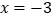 或
或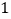 时,
时,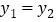 ;②当
;②当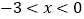 或
或 时,
时,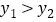 ,即通过观察函数的图象,可以得到不等式
,即通过观察函数的图象,可以得到不等式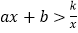 的解集.
的解集.有这样一个问题:求不等式
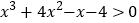 的解集.
的解集.某同学根据学习以上知识的经验,对求不等式
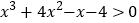 的解集进行了探究.
的解集进行了探究.下面是他的探究过程,请将(
 )、(
)、( )、(
)、( )补充完整:
)补充完整:(
 )将不等式按条件进行转化:
)将不等式按条件进行转化:当
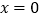 时,原不等式不成立.
时,原不等式不成立.当
 时,原不等式可以转化为
时,原不等式可以转化为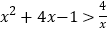 .
.当
 时,原不等式可以转化为
时,原不等式可以转化为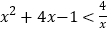 .
.(
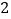 )构造函数,画出图象.
)构造函数,画出图象.设
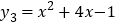 ,
,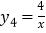 ,在同一坐标系中分别画出这两个函数的图象.
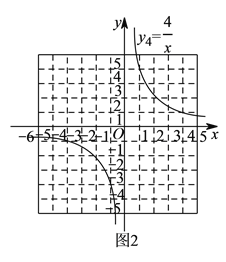
,在同一坐标系中分别画出这两个函数的图象.双曲线
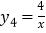 如图
如图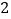 所示,请在此坐标系中画出抛物线
所示,请在此坐标系中画出抛物线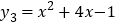 .(不用列表)
.(不用列表)(
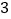 )确定两个函数图象公共点的横坐标.
)确定两个函数图象公共点的横坐标.观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足
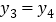 的所有
的所有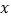 的值为__________.
的值为__________.(
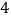 )借助图象,写出解集.
)借助图象,写出解集.结合(
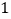 )的讨论结果,观察两个函数的图象可知:不等式
)的讨论结果,观察两个函数的图象可知:不等式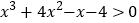 的解集为__________.
的解集为__________.
相关试题

