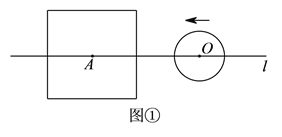
【题目】设边长为![]() 的正方形的中心
的正方形的中心![]() 在直线
在直线![]() 上,它的一组对边垂直于直线
上,它的一组对边垂直于直线![]() ,半径为
,半径为![]() 的圆的圆心
的圆的圆心![]() 在直线
在直线![]() 上运动,
上运动,![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() .
.
(![]() )如图①,当
)如图①,当![]() 时,填表:
时,填表:
| ⊙ |
|
|
|
|
| __________ |
| __________ |
| __________ |
(![]() )如图②,⊙
)如图②,⊙![]() 与正方形有
与正方形有![]() 个公共点
个公共点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,求此时
,求此时![]() 与
与![]() 之间的数量关系:
之间的数量关系:

(![]() )由(
)由(![]() )可知,
)可知,![]() 、
、![]() 、
、![]() 之间的数量关系和⊙
之间的数量关系和⊙![]() 与正方形的公共点个数密切相关.当
与正方形的公共点个数密切相关.当![]() 时,请根据
时,请根据![]() 、
、![]() 、
、![]() 之间的数量关系,判断⊙
之间的数量关系,判断⊙![]() 与正方形的公共点个数.
与正方形的公共点个数.
(![]() )当
)当![]() 与
与![]() 之间满足(
之间满足(![]() )中的数量关系时,⊙
)中的数量关系时,⊙![]() 与正方形的公共点个数为__________.
与正方形的公共点个数为__________.
参考答案:
【答案】 2 1 0 5
【解析】试题分析:(1)利用圆直线位置关系可得结果.(2) 连接![]() ,在
,在![]() 中,由勾股定理a与r的关系.(3) 当
中,由勾股定理a与r的关系.(3) 当![]() 时,⊙
时,⊙![]() 的直径等于正方形的边长, 与正方形一边相切,相交,与正方形四边形相切,四种情况.(4) 由(
的直径等于正方形的边长, 与正方形一边相切,相交,与正方形四边形相切,四种情况.(4) 由(![]() )中的数易关系,即
)中的数易关系,即![]() ,⊙
,⊙![]() 与正方形的公共点个数为
与正方形的公共点个数为![]() 个.
个.
试题解析:
(![]() )解:当
)解:当![]() 时,
时,![]() 的直径小于正方形的边长,
的直径小于正方形的边长,
![]() 与正方形中垂直于直线
与正方形中垂直于直线![]() 的一边相离、相切、相交,三种情况,
的一边相离、相切、相交,三种情况,
故可确定⊙![]() 与正方形的公共点的个数可能有
与正方形的公共点的个数可能有![]() 、
、![]() 、
、![]() 个.
个.
(![]() )如图所示,连接
)如图所示,连接![]() ,
,
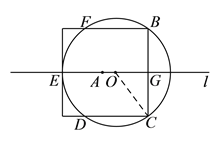
则![]() ,
,![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]() ,
,
即![]() span>,
span>,
![]() ,
,
![]() ,
,
![]() .
.
(![]() )当
)当![]() 时,⊙
时,⊙![]() 的直径等于正方形的边长,
的直径等于正方形的边长,
此时会出现![]() 与正方形相离,与正方形一边相切,相交,与正方形四边形相切,四种情况,
与正方形相离,与正方形一边相切,相交,与正方形四边形相切,四种情况,
故可确定⊙![]() 与正方形的交点个数可能有
与正方形的交点个数可能有![]() 、
、![]() 、
、![]() 、
、![]() 个.
个.
(![]() )由(
)由(![]() )中的数易关系,
)中的数易关系,
即![]() ,
,
⊙![]() 与正方形的公共点个数为
与正方形的公共点个数为![]() 个.
个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数
中位数
方差
甲
8
乙
8
2
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)
-
科目: 来源: 题型:
查看答案和解析>> -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
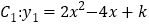 与
与 轴只有一个公共点.
轴只有一个公共点.(
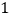 )求
)求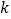 的值.
的值.(
 )怎样平移抛物线
)怎样平移抛物线 就可以得到抛物线
就可以得到抛物线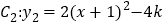 ?请写出具体的平移方法.
?请写出具体的平移方法.(
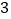 )若点
)若点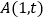 和点
和点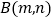 都在抛物线
都在抛物线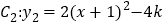 上,且
上,且 ,直接写出
,直接写出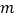 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
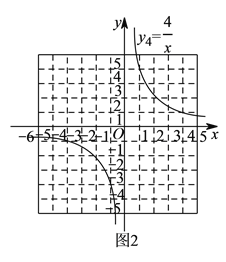
如图
 ,在平面直角坐标系
,在平面直角坐标系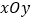 中,直线
中,直线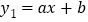 与双曲线
与双曲线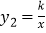 交于
交于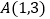 和
和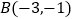 两点.
两点.观察图象可知:①当
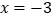 或
或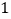 时,
时,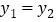 ;②当
;②当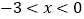 或
或 时,
时,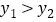 ,即通过观察函数的图象,可以得到不等式
,即通过观察函数的图象,可以得到不等式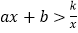 的解集.
的解集.有这样一个问题:求不等式
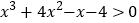 的解集.
的解集.某同学根据学习以上知识的经验,对求不等式
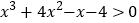 的解集进行了探究.
的解集进行了探究.下面是他的探究过程,请将(
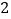 )、(
)、(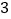 )、(
)、(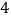 )补充完整:
)补充完整:(
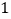 )将不等式按条件进行转化:
)将不等式按条件进行转化:当
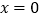 时,原不等式不成立.
时,原不等式不成立.当
 时,原不等式可以转化为
时,原不等式可以转化为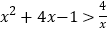 .
.当
 时,原不等式可以转化为
时,原不等式可以转化为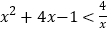 .
.(
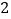 )构造函数,画出图象.
)构造函数,画出图象.设
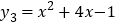 ,
,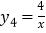 ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.双曲线
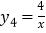 如图
如图 所示,请在此坐标系中画出抛物线
所示,请在此坐标系中画出抛物线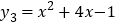 .(不用列表)
.(不用列表)(
 )确定两个函数图象公共点的横坐标.
)确定两个函数图象公共点的横坐标.观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足
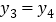 的所有
的所有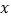 的值为__________.
的值为__________.(
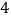 )借助图象,写出解集.
)借助图象,写出解集.结合(
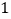 )的讨论结果,观察两个函数的图象可知:不等式
)的讨论结果,观察两个函数的图象可知:不等式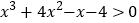 的解集为__________.
的解集为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图,在△
 中,把
中,把 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得到
得到 ,把
,把 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 得到
得到 ,连接
,连接 ,当
,当 时,我们称△
时,我们称△ 是△
是△ 的“旋补三角形”,△
的“旋补三角形”,△ 边
边 上的中线
上的中线 叫做
叫做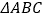 的“旋补中线”,点
的“旋补中线”,点 叫做“旋补中心”.
叫做“旋补中心”.⑴ 特例感知:在如图、如图中,
 是
是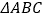 的“旋补三角形”,
的“旋补三角形”, 是
是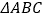 的“旋补中线”.
的“旋补中线”.① 如图,当
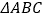 为等边三角形时,
为等边三角形时, 与
与 的数量关系为
的数量关系为 =
=  ;
;② 如图,当
 ,
, 时,则
时,则 长为 .
长为 .⑵ 精确作图:如图,已知在四边形
 内部存在点
内部存在点 ,使得
,使得 是
是 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点 (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)⑶ 猜想论证:在如图中,当△
 为任意三角形时,猜想
为任意三角形时,猜想 与
与 的数量关系,并给予证明.
的数量关系,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________,
 =________%,
=________%,  =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
相关试题

