【题目】如图,△ABC是直角三角形,∠ACB=90°.
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母;
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求![]() 的长.
的长.

参考答案:
【答案】(1)作图见试题解析;(2)![]() .
.
【解析】
试题分析:(1)过点C作CD⊥AB的于D,然后以C点为圆心,CD为半径作圆即可;
(2)由切线的性质得∠ADC=90°,利用互余可得∠DCE和∠BCD=的度数,在Rt△BCD中利用∠BCD的余弦可计算出CD的长,然后根据弧长公式求解.
试题解析:(1)如图,
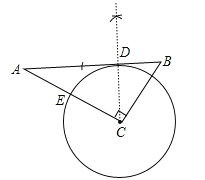
⊙C为所求;
(2)∵⊙C切AB于D,∴CD⊥AB,∴∠ADC=90°,∴∠DCE=90°﹣∠A=90°﹣30°=60°,∴∠BCD=90°﹣∠ACD=30°,在Rt△BCD中,∵cos∠BCD=![]() ,∴CD=3cos30°=
,∴CD=3cos30°=![]() ,∴
,∴![]() 的长=
的长=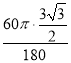 =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然事件的为( )
A.购买一张彩票,中奖
B.通常加热到100℃时,水沸腾
C.任意画一个三角形,其内角和是360°
D.射击运动员射击一次,命中靶心 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强对校内外安全监控,创建荔湾平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型
乙型
价格(元/台)
a
b
有效半径(米/台)
150
100
(1)求a、b的值.
(2)若购买该批设备的资金不超过11000元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(3)在(2)问的条件下,若要求监控半径覆盖范围不低于1600米,为了节约资金,请你设计一种最省钱的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:

②该产品90天内每天的销售价格与时间(第x天)的关系如下表:

(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格﹣每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程3﹣5(x+2)=x去括号正确的是( )
A.3﹣x+2=x
B.3﹣5x﹣10=x
C.3﹣5x+10=x
D.3﹣x﹣2=x -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.﹣2x2y3xy2=﹣6x2y2
B.(﹣x﹣2y)(x+2y)=x2﹣4y2
C.6x3y2÷2x2y=3xy
D.(4x3y2)2=16x9y4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形ABCD中,M为AB的中点,N为AD上的一点,且AN=
 AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角)
AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角) 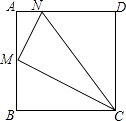
相关试题

