搜索
【题目】解方程3﹣5（x+2）=x去括号正确的是（ ）
A.3﹣x+2=x
B.3﹣5x﹣10=x
C.3﹣5x+10=x
D.3﹣x﹣2=x
参考答案：
【答案】B
【解析】解：去括号得：3﹣5x﹣10=x，
故选B．
【考点精析】掌握解一元一次方程的步骤是解答本题的根本，需要知道先去分母再括号，移项变号要记牢．同类各项去合并，系数化“1”还没好．求得未知须检验，回代值等才算了．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了加强对校内外安全监控，创建荔湾平安校园，某学校计划增加15台监控摄像设备，现有甲、乙两种型号的设备，其中每台价格，有效监控半径如表所示，经调查，购买1台甲型设备比购买1台乙型设备多150元，购买2台甲型设备比购买3台乙型设备少400元．
甲型
乙型
价格（元/台）
a
b
有效半径（米/台）
150
100
（1）求a、b的值．
（2）若购买该批设备的资金不超过11000元，且两种型号的设备均要至少买一台，学校有哪几种购买方案？
（3）在（2）问的条件下，若要求监控半径覆盖范围不低于1600米，为了节约资金，请你设计一种最省钱的购买方案． -
科目： 来源： 题型：
查看答案和解析>>【题目】某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：
（1）求m关于x的一次函数表达式；
（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格﹣每件成本）】
（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC是直角三角形，∠ACB=90°．
（1）尺规作图：作⊙C，使它与AB相切于点D，与AC相交于点E，保留作图痕迹，不写作法，请标明字母；
（2）在你按（1）中要求所作的图中，若BC=3，∠A=30°，求
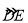的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算正确的是（ ）
A.﹣2x2y3xy2=﹣6x2y2
B.（﹣x﹣2y）（x+2y）=x2﹣4y2
C.6x3y2÷2x2y=3xy
D.（4x3y2）2=16x9y4 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在正方形ABCD中，M为AB的中点，N为AD上的一点，且AN=
AD，试猜测△CMN是什么三角形，请证明你的结论．（提示：正方形的四条边都相等，四个角都是直角）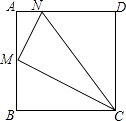 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1所示，已知抛物线
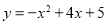的顶点为D，与x轴交于A、B两点，与y轴交于C点，E为对称轴上的一点，连接CE，将线段CE绕点E按逆时针方向旋转90°后，点C的对应点C′恰好落在y轴上．（1）直接写出D点和E点的坐标；
（2）点F为直线C′E与已知抛物线的一个交点，点H是抛物线上C与F之间的一个动点，若过点H作直线HG与y轴平行，且与直线C′E交于点G，设点H的横坐标为m（0＜m＜4），那么当m为何值时，
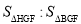=5：6？（3）图2所示的抛物线是由
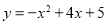向右平移1个单位后得到的，点T（5，y）在抛物线上，点P是抛物线上O与T之间的任意一点，在线段OT上是否存在一点Q，使△PQT是等腰直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．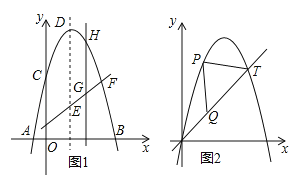
相关试题
