【题目】如图所示,在正方形ABCD中,M为AB的中点,N为AD上的一点,且AN= ![]() AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角)
AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角) 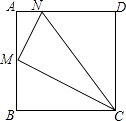
参考答案:
【答案】解:△CMN是直角三角形.理由如下: 设正方形ABCD的边长为4a,则AB=BC=CD=AD=4a.
∵M是AB的中点,
∴AM=BM=2a.
∵AN= ![]() AD,AD=4a,
AD,AD=4a,
∴AN=a,DN=3a.
∵在Rt△AMN中,满足AM2+AN2=MN2 , 且AM=2a,AN=a,
∴MN= ![]() a.
a.
同理可得:MC= ![]() a,NC=5a.
a,NC=5a.
∵MN2+MC2=( ![]() a)2+(
a)2+( ![]() a)2=25a2 , NC2=(5a)2=25a2 ,
a)2=25a2 , NC2=(5a)2=25a2 ,
∴MN2+MC2=NC2 ,
∴△CMN是直角三角形
【解析】可设正方形ABCD的边长为4a,利用勾股定理分别求出NC,MN,CM的值,计算得出MN2+MC2=NC2 , 根据勾股定理的逆定理可判定△CMN是直角三角形.
【考点精析】利用勾股定理的概念和勾股定理的逆定理对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是直角三角形,∠ACB=90°.
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母;
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求
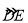 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程3﹣5(x+2)=x去括号正确的是( )
A.3﹣x+2=x
B.3﹣5x﹣10=x
C.3﹣5x+10=x
D.3﹣x﹣2=x -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.﹣2x2y3xy2=﹣6x2y2
B.(﹣x﹣2y)(x+2y)=x2﹣4y2
C.6x3y2÷2x2y=3xy
D.(4x3y2)2=16x9y4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知抛物线
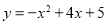 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,
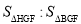 =5:6?
=5:6?(3)图2所示的抛物线是由
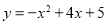 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.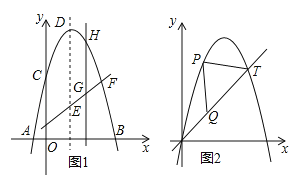
-
科目: 来源: 题型:
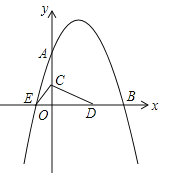
查看答案和解析>>【题目】如图,已知抛物线
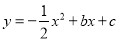 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年我国约有9400000人参加高考,将9400000用科学记数法表示为 .
相关试题

