【题目】已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣ ![]() x+b与抛物线的另一个交点为D.
x+b与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒 ![]() 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
参考答案:
【答案】
(1)
解:∵y=a(x+3)(x﹣1),
∴点A的坐标为(﹣3,0)、点B两的坐标为(1,0),
∵直线y=﹣ ![]() x+b经过点A,
x+b经过点A,
∴b=﹣3 ![]() ,
,
∴y=﹣ ![]() x﹣3
x﹣3 ![]() ,
,
当x=2时,y=﹣5 ![]() ,
,
则点D的坐标为(2,﹣5 ![]() ),
),
∵点D在抛物线上,
∴a(2+3)(2﹣1)=﹣5 ![]() ,
,
解得,a=﹣ ![]() ,
,
则抛物线的解析式为y=﹣ ![]() (x+3)(x﹣1)=﹣
(x+3)(x﹣1)=﹣ ![]() x2﹣2
x2﹣2 ![]() x+3
x+3 ![]()
(2)
解:如图1中,作PH⊥x轴于H,设点 P坐标(m,n),
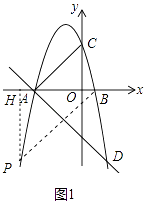
当△BPA∽△ABC时,∠BAC=∠PBA,
∴tan∠BAC=tan∠PBA,即 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即n=﹣a(m﹣1),
,即n=﹣a(m﹣1),
∴ ![]() 解得m=﹣4或1(舍弃),
解得m=﹣4或1(舍弃),
当m=﹣4时,n=5a,
∵△BPA∽△ABC,
∴ ![]() =
= ![]() ,
,
∴AB2=ACPB,
∴42= ![]() ,
,
解得a=﹣ ![]() 或
或 ![]() (舍弃),
(舍弃),
则n=5a=﹣ ![]() ,
,
∴点P坐标(﹣4,﹣ ![]() ).
).
当△PBA∽△ABC时,∠CBA=∠PBA,
∴tan∠CBA=tan∠PBA,即 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴n=﹣3a(m﹣1),
∴ ![]() ,
,
解得m=﹣6或1(舍弃),
当m=﹣6时,n=21a,
∵△PBA∽△ABC,
∴ ![]() =
= ![]() ,即AB2=BCPB,
,即AB2=BCPB,
∴42= ![]()
![]() ,
,
解得a=﹣ ![]() 或
或 ![]() (不合题意舍弃),
(不合题意舍弃),
则点P坐标(﹣6,﹣3 ![]() ),
),
综上所述,符合条件的点P的坐标(﹣4,﹣ ![]() )和(﹣6,﹣3
)和(﹣6,﹣3 ![]() ).
).
(3)
解:如图2中,作DM∥x轴交抛物线于M,作DN⊥x轴于N,作EF⊥DM于F,
则tan∠DAN= ![]() =
= ![]() =
= ![]() ,
,
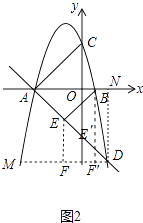
∴∠DAN=60°,
∴∠EDF=60°,
∴DE= ![]() =
= ![]() EF,
EF,
∴Q的运动时间t= ![]() +
+ ![]() =BE+EF,
=BE+EF,
∴当BE和EF共线时,t最小,
则BE⊥DM,此时点E坐标(1,﹣4 ![]() )
)
【解析】(1)根据二次函数的交点式确定点A、B的坐标,进而求出直线AD的解析式,接着求出点D的坐标,将D点坐标代入抛物线解析式确定a的值;(2)由于没有明确说明相似三角形的对应顶点,因此需要分情况讨论:①△ABC∽△BAP;②△ABC∽△PAB;(3)作DM∥x轴交抛物线于M,作DN⊥x轴于N,作EF⊥DM于F,根据正切的定义求出Q的运动时间t=BE+EF时,t最小即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七中育才学校排球活动月即将开始,其中有一项为垫球比赛,体育组为了了解七年级学生的训练情况,随机抽取了七年级部分学生进行1分钟垫球测试,并将这些学生的测试成绩(即1分钟的个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级,90~120范围内的记为C级,120~150范围内的记为B级,150~180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题:
(1)在扇形统计图中,A级所占百分比为 ;
(2)在这次测试中,一共抽取了 名学生,并补全频数分布直方图;
(3)在(2)中的基础上,在扇形统计图中,求D级对应的圆心角的度数;
(4)若A,B,C,D等级的平均成绩分别为165、135、105、75个,你能估算出学校七年级同学的平均水平吗?若能,请计算出来.(保留准确值)

-
科目: 来源: 题型:
查看答案和解析>>【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.

(1)如图1,当tan∠PAB=1,c=4 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3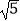 ,AB=3,求AF的长.
,AB=3,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是矩形
是矩形 对角线的交点,
对角线的交点, ,
, .
.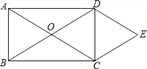
 求证:四边形
求证:四边形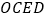 是菱形.
是菱形.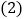 若
若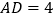 ,
,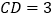 ,求四边形
,求四边形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D,F在x轴上,点C在DE边上,反比例函数y=
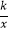 (k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )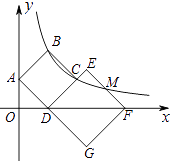
A.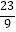
B.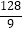
C.16
D.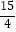
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程:①3x﹣1=2x+1,②
 ,③
,③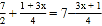 ,④
,④ x﹣1=x中,解为x=2的是方程( )
x﹣1=x中,解为x=2的是方程( )A. ①、②和③ B. ①、③和④ C. ②、③和④ D. ①、②和④
-
科目: 来源: 题型:
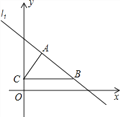
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
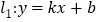 经过第一象限的点
经过第一象限的点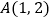 和点
和点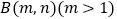 ,且
,且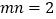 ,过点
,过点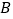 作
作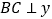 轴,垂足为
轴,垂足为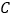 ,
,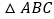 的面积为
的面积为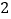 .
.
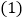 求
求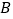 点的坐标;
点的坐标;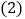 求直线
求直线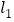 的函数表达式;
的函数表达式; 直线
直线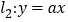 经过线段
经过线段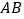 上一点
上一点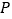 (
(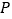 不与
不与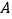 、
、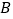 重合),求
重合),求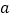 的取值范围.
的取值范围.
相关试题

