【题目】为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图: 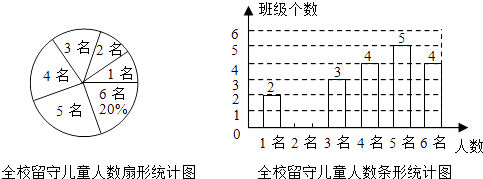
(1)将该条形统计图补充完整;
(2)求该校平均每班有多少名留守儿童?
(3)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
参考答案:
【答案】
(1)解:该校班级个数为4÷20%=20(个),
只有2名留守儿童的班级个数为:20﹣(2+3+4+5+4)=2(个),
补图如下:
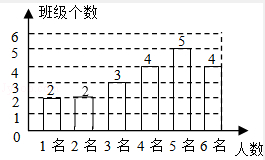
(2)解:该校平均每班留守儿童的人数为:
(1×2+2×2+3×3+4×4+5×5+6×4)÷20=4(个);
(3)解:由(1)得只有2名留守儿童的班级有2个,共4名学生,设A1,A2来自一个班,B1,B2来自一个班,如图;
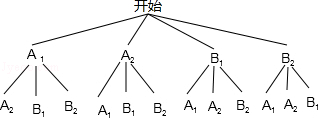
由树状图可知,共有12种可能的情况,并且每种结果出现的可能性相等,其中来自一个班的共有4种情况,
则所选两名留守儿童来自同一个班级的概率为: ![]() =
= ![]() .
.
【解析】(1)根据留守儿童有6名的班级占20%,可求得有留守儿童的总班级数,再减去其它班级数,即可补全统计图;(2)根据班级个数和班级人数,求出总的留守儿童数,再除以总班级数,即可得出答案;(3)根据(1)可知,只有2名留守儿童的班级有2个,共4名学生,再设A1 , A2来自一个班,B1 , B2来自一个班,列出树状图可得出来自一个班的共有4种情况,再根据概率公式即可得出答案.
-
科目: 来源: 题型:
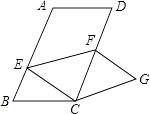
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G,则△CEF的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副直角三角尺叠放如图 1 所示,现将 45°的三角尺ADE 固定不动,将含 30°的三角尺 ABC 绕顶点 A 顺时针转动(旋转角不超过 180 度),使两块三角尺至少有一组边互相平行.如图 2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠EFC+∠BDC=180°,∠DEF=∠B.
(1)求证:∠ADE=∠DEF;
(2)判定 DE 与 BC 的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
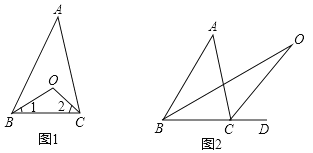
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+
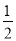 ∠A,理由如下:
∠A,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=
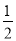 ∠ABC,∠2=
∠ABC,∠2=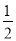 ∠ACB.
∠ACB.∴∠1+∠2=
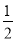 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= 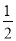 (180°-∠A)=90°-
(180°-∠A)=90°- ∠A.
∠A.∴∠BOC=180°-(∠1+∠2)=180°-(90°-
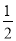 ∠A)=90°+
∠A)=90°+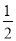 ∠A
∠A探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC.
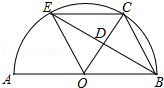
(1)求证:△BDO≌△EDC.
(2)若OB=6,则四边形OBCE的面积为 . -
科目: 来源: 题型:
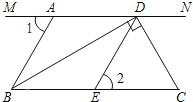
查看答案和解析>>【题目】如图,MN∥BC,BD⊥DC,∠1=∠2=60°.
(1)AB 与 DE 平行吗?请说明理由;
(2)若 DC 是∠NDE 的平分线.
①试说明∠ABC=∠C;
②试说明 BD 是∠ABC 的平分线.
相关试题

