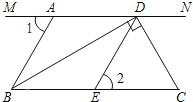
【题目】如图,MN∥BC,BD⊥DC,∠1=∠2=60°.
(1)AB 与 DE 平行吗?请说明理由;
(2)若 DC 是∠NDE 的平分线.
①试说明∠ABC=∠C;
②试说明 BD 是∠ABC 的平分线.
参考答案:
【答案】(1)AB∥DE,理由见解析;(2)见解析.
【解析】(1)首先根据平行线的性质,两直线平行,内错角相等即可证得∠ABC=∠1=60°,进而证明∠ABC=∠2,根据同位角相等,两直线平行,即可证得;
(2)①根据平行线的性质,两直线平行,同旁内角互补求得∠NDE的度数,然后根据角平分线的定义,以及平行线的性质即可求得∠C的度数,从而判断;
②在直角△BCD中,求得∠DBC的度数,然后求得∠ABD的度数,即可证得.
(1)AB∥DE,理由如下:
∵MN∥BC( 已知 ),
∴∠ABC=∠1=60°( 两直线平行,内错角相等 ).
又∵∠1=∠2( 已知 ).
∴∠ABC=∠2( 等量代换 ).
∴AB∥DE( 同位角相等,两直线平行 );
(2)①∵MN∥BC,
∴∠NDE+∠2=180°,
∴∠NDE=180°﹣∠2=180°﹣60°=120°.
∵DC 是∠NDE 的平分线,
∴∠EDC=∠NDC=![]() ∠NDE=60°.
∠NDE=60°.
∵MN∥BC,
∴∠C=∠NDC=60°.
∴∠ABC=∠C.
②∠ADC=180°﹣∠NDC=180°﹣60°=120°,
∵BD⊥DC,
∴∠BDC=90°.
∴∠ADB=∠ADC﹣∠BDC=120°﹣90°=30°.
∵MN∥BC,
∴∠DBC=∠ADB=30°.
∴∠ABD=∠DBC=![]() ∠ABC.
∠ABC.
∴BD 是∠ABC 的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图:
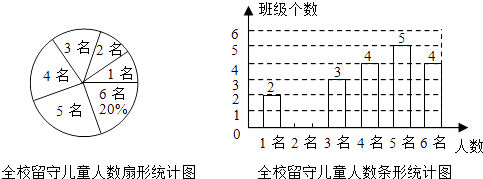
(1)将该条形统计图补充完整;
(2)求该校平均每班有多少名留守儿童?
(3)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+
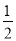 ∠A,理由如下:
∠A,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=
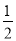 ∠ABC,∠2=
∠ABC,∠2=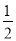 ∠ACB.
∠ACB.∴∠1+∠2=
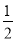 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= 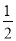 (180°-∠A)=90°-
(180°-∠A)=90°- ∠A.
∠A.∴∠BOC=180°-(∠1+∠2)=180°-(90°-
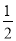 ∠A)=90°+
∠A)=90°+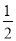 ∠A
∠A探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
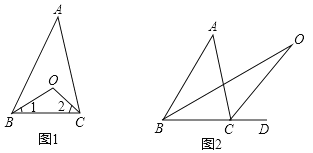
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC.
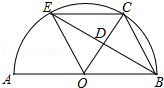
(1)求证:△BDO≌△EDC.
(2)若OB=6,则四边形OBCE的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:
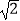 ≈1.41,
≈1.41, 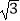 ≈1.73,结果保留整数)
≈1.73,结果保留整数) 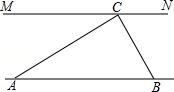
-
科目: 来源: 题型:
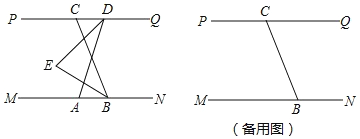
查看答案和解析>>【题目】如图,已知 MN∥PQ,B 在 MN 上,C 在 PQ 上,A 在 B 的左侧,D 在 C 的右侧,DE 平分∠ADC,BE平分∠ABC,直线 DE,BE 交于点 E,∠CBN=120°.
(1)若∠ADQ=110°,求∠BED 的度数;
(2)将线段 AD 沿 DC 方向平移,使得点 D 在点 C 的左侧,其他条件不变,若∠ADQ=n°,求∠BED 的度数(用含 n 的代数式表示)
相关试题

