【题目】如图,∠COD=45°,∠BOD=![]() ∠COD,OC是∠AOB的平分线,求∠AOD的度数.
∠COD,OC是∠AOB的平分线,求∠AOD的度数.
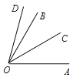
参考答案:
【答案】75°.
【解析】
解法一:先根据∠COD=45°,∠BOD=![]() ∠COD求出∠BOD,∠COB的度数,再利用角平分线可求出∠AOB,最后利用∠AOD=∠BOD+∠AOB即可求解.
∠COD求出∠BOD,∠COB的度数,再利用角平分线可求出∠AOB,最后利用∠AOD=∠BOD+∠AOB即可求解.
解法二:先根据∠COD=45°,∠BOD=![]() ∠COD求出∠BOD,∠COB的度数,再利用角平分线可求出∠AOC的度数,最后利用∠AOD=∠COD+∠AOC即可求解.
∠COD求出∠BOD,∠COB的度数,再利用角平分线可求出∠AOC的度数,最后利用∠AOD=∠COD+∠AOC即可求解.
解法一:∵∠COD=45°,∠BOD=![]() ∠COD,
∠COD,
∴∠BOD=![]() ×45° =15°.
×45° =15°.
∴∠COB=∠COD-∠BOD=45°-15°=30°.
∵OC是∠AOB的平分线,
∴∠AOB=2∠COB=2×30°=60°
∴∠AOD=∠BOD+∠AOB=15°+60°=75°.
解法二:∵∠COD=45°,∠BOD=![]() ∠COD,
∠COD,
∴∠BOD=![]() ×45° =15°.
×45° =15°.
∴∠COB=∠COD-∠BOD=45°-15°=30°.
∵OC是∠AOB的平分线,
∴∠AOC=∠COB=30°
∴∠AOD=∠COD+∠AOC=45°+30°=75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
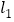 ∥
∥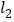 ,BE∥CF,BA⊥
,BE∥CF,BA⊥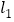 ,DC⊥
,DC⊥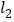 ,下面给出四个结论:①BE=CF;②AB=DC;③
,下面给出四个结论:①BE=CF;②AB=DC;③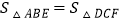 ;
;④四边形ABCD是矩形.其中说法正确的有( )
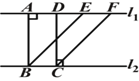
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到位于码头A正东方向的码头B,测得小岛C位于码头B的北偏西53°方向,求码头A与码头B的距离.【参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.42,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】

-
科目: 来源: 题型:
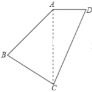
查看答案和解析>>【题目】如图,在四边形ABCD中,AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,则∠DAB的度数是______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在精准扶贫政策的扶持下,贫困户老李今年试种的百香果获得大丰收,共收获2 000千克.扶贫小组帮助他将百香果按照品质从高到低分成A,B,C,D,E五个等级,并根据数据绘制了如下的扇形统计图和频数分布表:

请根据图表信息解答下列问题:
(1)
 __________;
__________; __________;
__________; __________;
__________;(2)求扇形统计图中“E”所对应的圆心角的度数;
(3)为了帮助贫困户老李销售百香果,扶贫小组联系了甲、乙两位经销商.他们分别给出如下收购方案:
甲:全部按5元/千克收购;
乙:按等级收购:C等级单价为6.5元/千克,每提高一个等级单价提高1元/千克,剩下的D,E两个等级单价均为2元/千克.
请你通过计算,判断哪个经销商的方案使老李盈利更多.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=
 ,求AB的长。
,求AB的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.

(1)求证:△ADG≌△CDG.
(2)若
 =
= ,EG=4,求AG的长.
,EG=4,求AG的长.
相关试题

