【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
参考答案:
【答案】解:(1)证明:∵四边形ABCD是矩形,∴DC∥AB。
∴∠OAE=∠OCF,∠OEA=∠OFC。
又∵AE=CF,∴△OEA≌△OFC(ASA)。
∴OE=OF。
(2)如图,连接OB,
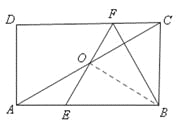
∵BE=BF,OE=OF,∴BO⊥EF,∠ABO=∠OBF。
∵∠BEF=2∠BAC,∴∠OBE=∠BAC。
又∵矩形ABCD中,∠ABC=900,∴∠BOE=∠ABC=900。
∴△OBE∽△BAC。∴![]() 。
。
∵∠BEF=2∠BAC,∴∠OAE=∠AOE。∴AE=OE。
设AB=x,AE=OE=y,则![]() 。
。
∵BC=![]() ,∴
,∴![]() 。
。
由(1)△OEA≌△OFC,得AO=CO,∴![]() 。
。
∴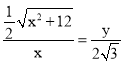 。∴
。∴![]() ①。
①。
又∵![]() ,即
,即![]() ,
,
化简,得![]() ②。
②。
由①②得![]() ,两边平方并化简,得
,两边平方并化简,得![]() ,
,
∴![]() ,∴根据x的实际意义,得x=6。
,∴根据x的实际意义,得x=6。
∴若BC=![]() , AB的长为6。
, AB的长为6。
【解析】试题分析:(1)根据△AEO和△CFO全等来进行说明;(2)连接OB,得出△BOF和△BOE全等,然后求出∠BAC的度数,根据∠BAC的正切值求出AB的长度.
试题解析:(1)∵四边形ABCD是矩形,∴AB∥CD ∴∠OAE=∠OCF ∠OEA=∠OFC ∵AE=CF
∴△AEO≌△CFO ∴OE=OF
(2)连接BO ∵OE=OF BE=BF
∴BO⊥EF 且∠EBO=∠FBO ∴∠BOF=90°
∵四边形ABCD是矩形
∴∠BCF=90°
∵∠BEF=2∠BAC ∠BEF=∠BAC+∠EOA
∴∠BAC=∠EOA AE=OE
∵AE=CF OE=OF
∴OF=CF 又∵BF=BF
∴Rt△BOF≌Rt△BCF
∴∠OBF=∠CBF
∴∠CBF=∠FBO=∠OBE
∵∠ABC=90° ∠OBE=30°
∴∠BEO=60° ∠BAC=30°
∵tan∠BAC=![]()
∴tan30°=![]() 即
即![]() ∴AB=6.
∴AB=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
 的正方形
的正方形 中,点
中,点 在
在 上从
上从 向
向 运动,连接
运动,连接 交
交 于点
于点 .
.(
 )试证明:无论点
)试证明:无论点 运动到
运动到 上何处时,都有
上何处时,都有 ≌
≌ .
.(
 )若点
)若点 从点
从点 运动到点
运动到点 ,再继续在
,再继续在 上运动到点
上运动到点 ,在整个运动过程中,点
,在整个运动过程中,点 以每秒
以每秒 单位长度的速度匀速运动,当
单位长度的速度匀速运动,当 恰为等腰三角形,求点
恰为等腰三角形,求点 运动的时间.
运动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形
是等边三角形 内的一点,连结
内的一点,连结 、
、 、
、 ,以
,以 为边作
为边作 且
且 .连结
.连结 .
.(1)观察并猜想
 与
与 之间的大小关系,并证明你的结论.
之间的大小关系,并证明你的结论.(2)若
 ,
,  ,
,  ,连结
,连结 ,试判断
,试判断 的形状,并说明理由.
的形状,并说明理由.(3)在(2)的条件下,求
 的面积.
的面积.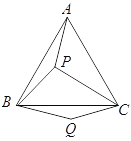
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(x4)3+(x3)4﹣2x4x8
-
科目: 来源: 题型:
查看答案和解析>>【题目】把角度化为度、分的形式,则20.5°=20°′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左到右的变形中,是因式分解的为( )
A. ab+ac+d=a(b+c)+dB. (x+2)(x﹣2)=x2﹣4
C. 6ab=2a3bD. x2﹣8x+16=(x﹣4)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】对应命题“若
 ,则
,则 ”,下面四组
”,下面四组 ,
,  的值中,能说明这个命题是假命题的是( ).
的值中,能说明这个命题是假命题的是( ).A.
 ,
,  B.
B.  ,
,  C.
C.  ,
,  D.
D. 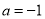 ,
, 
相关试题

