【题目】综合与探究
(实践操作)三角尺中的数学
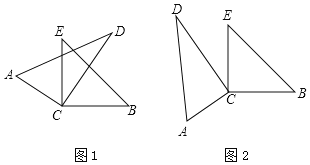
数学实践活动课上,“奋进”小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
(问题发现)
(1)①填空:如图1,若∠ACB=145°,则∠ACE的度数是 ,∠DCB的度数 ,∠ECD的度数是 .
②如图1,你发现∠ACE与∠DCB的大小有何关系?∠ACB与∠ECD的大小又有何关系?请直接写出你发现的结论.
(类比探究)
(2)如图2,当△ACD与△BCE没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
参考答案:
【答案】(1)①55°, 55°, 35°;②∠ACE=∠DCB,∠ACB+∠ECD=180°;(2)当△ACD与△BCE没有重合部分时,上述②中发现的结论依然成立,理由详见解析
【解析】
(1)先计算出![]() ,再根据
,再根据![]() 即可求解;
即可求解;
(2)根据余角的性质可得![]() ,根据角的和差关系可得
,根据角的和差关系可得![]() ;
;
(3)利用周角定义得![]() ,而
,而![]() ,即可得到
,即可得到![]() .
.
解:(1)①![]() ,
,
![]() ;
;
②结论:![]() ,
,![]() ;
;
证明:∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
(2)结论:当![]() 与
与![]() 没有重合部分时,上述②中发现的结论依然成立.
没有重合部分时,上述②中发现的结论依然成立.
理由:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∴上述②中发现的结论依然成立.
故答案为:(1)①55°, 55°, 35°;②∠ACE=∠DCB,∠ACB+∠ECD=180°;(2)当△ACD与△BCE没有重合部分时,上述②中发现的结论依然成立,理由详见解析
-
科目: 来源: 题型:
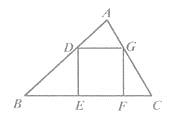
查看答案和解析>>【题目】如图,△ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上.若△ADG、△BED、△CFG的面积分别是1、3、1,则正方形的边长为( )
A.
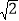 B.
B.  C. 2 D. 2
C. 2 D. 2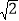
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AC的中点,点A、B在x轴上.若函数
 (x>0) 的图像过D、E两点,则矩形ABCD的面积为________.
(x>0) 的图像过D、E两点,则矩形ABCD的面积为________.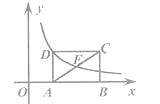
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝国庆节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
购买服装的套数
1套至45套
46套至90套
91套及以上
每套服装的价格
60元
50元
40元
如果两所学校分别单独购买服装,一共应付5000元.
(1)甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲、乙两所学校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市设计的长方形休闲广场如图所示,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池.
(1)用图中所标字母表示广场空地(图中阴影部分)的面积.
(2)若休闲广场的长为90米,宽为40米,求广场空地的面积(计算结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
(1)若他早上领取备用金4000元,那么下班时应交回银行_________元钱.
(2)请判断在这七次办理业务中,小张在第_______次业务办理后手中现金最多,第_________次业务办理后手中现金最少.
(3)若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
(4)若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.
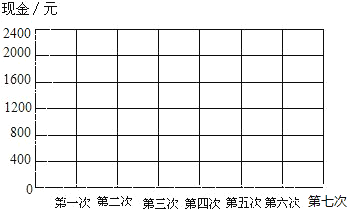
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ ABCD中,E是AD边上一点,AD=4
 ,CD=3,ED=
,CD=3,ED= ,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将
,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将  CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
相关试题

