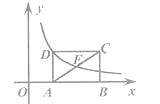
【题目】如图,矩形ABCD中,E是AC的中点,点A、B在x轴上.若函数![]() (x>0) 的图像过D、E两点,则矩形ABCD的面积为________.
(x>0) 的图像过D、E两点,则矩形ABCD的面积为________.
参考答案:
【答案】12
【解析】过E作EF⊥AB于F,由三角形中位线定理可得AD=2EF,设点D的横坐标为m,D点坐标为(m,![]() ),得出AD=
),得出AD=![]() ,即可得出EF=
,即可得出EF=![]() ,根据图象上的坐标特征得出E的横坐标为2m,继而得出AB=2m,然后根据矩形的面积公式即可求得.
,根据图象上的坐标特征得出E的横坐标为2m,继而得出AB=2m,然后根据矩形的面积公式即可求得.
过E作EF⊥AB于F,

∵点E是矩形ABCD对角线的交点,
∴AE=CE,
∴EF是△ABC的中位线,
∴AD=2EF,
设点D的横坐标为m,且点D在反比例函数y=![]() (x>0)上,
(x>0)上,
∴D点坐标为(m,![]() ),
),
∴AD=![]() ,
,
∴EF=![]() ,
,
∴F(2m,![]() ),
),
∴AF=m,
∴AB=2m,
∴矩形ABCD的面积=2m![]() =12,
=12,
故答案为12.
-
科目: 来源: 题型:
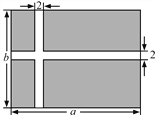
查看答案和解析>>【题目】 某公园准备修建一块长方形草坪,长为a米,宽为b米.并在草坪上修建如图所示的十字路,
已知十字路宽2米.
(1)用含a、b的代数式表示修建的十字路的面积.
(2)若a=30,b=20,求草坪(阴影部分)的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并解答问题:
数学大师的名题与方程
欧拉是18世纪瑞士著名的数学大师.他的一生都致力于数学各个领域的研究,并取得非凡的成就.在他所著的《代数学入门》一书中就曾经出现过好几道和遗产分配有关的数学问题.他构思这些问题的初衷,正是为了强化方程解题的适用和便利.
请用适当的方法解答下面问题:
父亲死后,四个儿子按下述方式分了他的财产:老大拿了财产的一半少3000英镑:老二拿了财产的
 少1000英镑;老三拿了恰好是财产的
少1000英镑;老三拿了恰好是财产的 ;老四拿了财产的
;老四拿了财产的 加上600英镑.问整个财产有多少?每个儿子各分了多少?
加上600英镑.问整个财产有多少?每个儿子各分了多少?
-
科目: 来源: 题型:
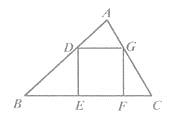
查看答案和解析>>【题目】如图,△ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上.若△ADG、△BED、△CFG的面积分别是1、3、1,则正方形的边长为( )
A.
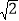 B.
B.  C. 2 D. 2
C. 2 D. 2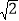
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝国庆节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
购买服装的套数
1套至45套
46套至90套
91套及以上
每套服装的价格
60元
50元
40元
如果两所学校分别单独购买服装,一共应付5000元.
(1)甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲、乙两所学校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
(实践操作)三角尺中的数学
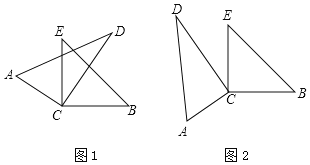
数学实践活动课上,“奋进”小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
(问题发现)
(1)①填空:如图1,若∠ACB=145°,则∠ACE的度数是 ,∠DCB的度数 ,∠ECD的度数是 .
②如图1,你发现∠ACE与∠DCB的大小有何关系?∠ACB与∠ECD的大小又有何关系?请直接写出你发现的结论.
(类比探究)
(2)如图2,当△ACD与△BCE没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市设计的长方形休闲广场如图所示,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池.
(1)用图中所标字母表示广场空地(图中阴影部分)的面积.
(2)若休闲广场的长为90米,宽为40米,求广场空地的面积(计算结果保留π).

相关试题

