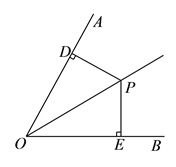
【题目】已知:如图, ![]() 是
是![]() 内一点,
内一点, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是垂足,且
分别是垂足,且![]() .
.
(![]() )求证:点
)求证:点![]() 在
在![]() 的平分线上.
的平分线上.
(![]() )若点
)若点![]() 是射线
是射线![]() 上一点,点
上一点,点![]() 是射线
是射线![]() 上一点,且
上一点,且![]() ,
, ![]() .
.
①当![]() 是等腰三角形时,求点
是等腰三角形时,求点![]() 到射线
到射线![]() 的距离;
的距离;
②连接![]() ,
, ![]() ,
, ![]() ,当
,当![]() 的周长最小时,求
的周长最小时,求![]() 的度数.
的度数.
参考答案:
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )①
)①![]() 或
或![]() 或
或![]() ;②
;②![]() .
.
【解析】试题分析:(1)证明![]() ≌
≌![]() ,根据全等三角形的对应角相等即可得;
,根据全等三角形的对应角相等即可得;
(2)①分![]() 或
或![]() 或
或![]() 三种情况进行讨论即可得;
三种情况进行讨论即可得;
②当![]() 为等边三角形时,
为等边三角形时, ![]() 周长最小,则
周长最小,则![]() .作点
.作点![]() 关于射线
关于射线![]() 的对应点
的对应点![]() ,关于射线
,关于射线![]() 的一应点
的一应点![]() ,连结
,连结![]()
![]() ,则线段
,则线段![]()
![]() 与
与![]() 的交点为
的交点为![]() .与
.与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() ,由两点之间线段最短,可知
,由两点之间线段最短,可知![]() 周小.
周小.
试题解析:(1)在![]() 和
和![]() 中,有
中,有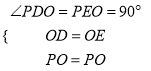 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 的平分线上;
的平分线上;
(2)①若![]() 是等腰三角形,则
是等腰三角形,则![]() 或
或![]() 或
或![]() .
.
(Ⅰ)若![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
∴![]() 到
到![]() 的距离为
的距离为![]() ;
;
(Ⅱ)若![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
∵![]() ,则
,则![]() ,
,
∴![]() .
.
∴![]() .
.
又![]() ,设
,设![]() ,
,
则![]() ,
,
即![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() ;
;
(Ⅲ)若![]() ,同理可知
,同理可知![]() .
.
综上,点![]() 到射线
到射线![]() 的距离为
的距离为![]() 或
或![]() 或
或![]() ;
;
②当![]() 为等边三角形时,
为等边三角形时, ![]() 周长最小,则
周长最小,则![]() .
.
作点![]() 关于射线
关于射线![]() 的对应点
的对应点![]() ,关于射线
,关于射线![]() 的一应点
的一应点![]() ,连结
,连结![]()
![]() ,则线段
,则线段![]()
![]() 与
与![]() 的交点为
的交点为![]() .与
.与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() ,由两点之间线段最短,可知
,由两点之间线段最短,可知![]() 周小.
周小.
如图所示:由轴对称性质可得,
OP1=OP2=OP,∠P1OA=∠POA,∠P2OB=∠POB,
所以∠P1OP2=2∠AOB=2×60°=120°,
所以∠OP1P2=∠OP2P1=(180°-120°)÷2=30°,
又因为∠FPO=∠OP1F=30°,∠GPO=∠OP2G=30°,
所以∠FPG=∠FPO+∠GPO=60°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
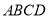 是一块边长为4米的正方形苗圃,园林部门将其改造为矩形
是一块边长为4米的正方形苗圃,园林部门将其改造为矩形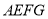 的形状,其中点
的形状,其中点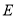 在
在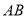 边上,点
边上,点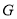 在
在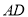 的延长线上,
的延长线上, 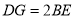 设
设 的长为
的长为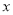 米,改造后苗圃
米,改造后苗圃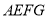 的面积为
的面积为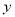 平方米.
平方米.(1)
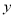 与
与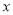 之间的函数关系式为 (不需写自变量的取值范围);
之间的函数关系式为 (不需写自变量的取值范围);(2)根据改造方案,改造后的矩形苗圃
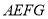 的面积与原正方形苗圃
的面积与原正方形苗圃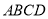 的面积相等,请问此时
的面积相等,请问此时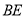 的长为多少米?
的长为多少米?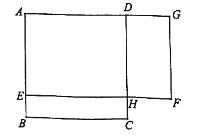
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+2)x﹣1=1,则x=_____.
-
科目: 来源: 题型:
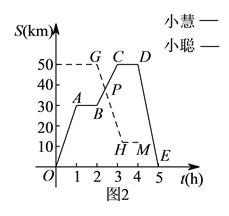
查看答案和解析>>【题目】小聪和小慧在某风景区(如图
 )沿景区公路游览,约好在宾馆见面.上午
)沿景区公路游览,约好在宾馆见面.上午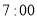 ,小慧乘坐车速为
,小慧乘坐车速为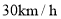 的电动汽车从宾馆出发,先后在两个景点游玩
的电动汽车从宾馆出发,先后在两个景点游玩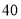 分钟和
分钟和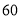 分钟后回到宾馆.小聪骑自行车从飞瀑出发,车速为
分钟后回到宾馆.小聪骑自行车从飞瀑出发,车速为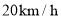 ,他先后在两个景点游玩了
,他先后在两个景点游玩了 分钟和
分钟和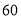 分钟后回到宾馆.图
分钟后回到宾馆.图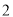 中的图象分别表示小慧和小聪离宾馆的路程
中的图象分别表示小慧和小聪离宾馆的路程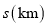 与时间
与时间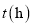 的函数关系(不全).试结合图中信息回答:
的函数关系(不全).试结合图中信息回答:(
 )小慧游览的景点是__________,点
)小慧游览的景点是__________,点 的坐标为__________.
的坐标为__________.(
 )当小聪和小慧相遇时,叫他们距离宾馆多少千米?
)当小聪和小慧相遇时,叫他们距离宾馆多少千米?
-
科目: 来源: 题型:
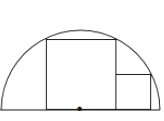
查看答案和解析>>【题目】如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为( )
A. (4+
 )cm B. 9cm C. 4
)cm B. 9cm C. 4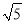 cm D. 6
cm D. 6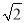 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】下面4个说法中,正确的个数为( ).
(1)“从袋中取出一只红球的概率是99%”,这句话的意思是肯定会取出一只红球,因为概率已经很大
(2)袋中有红、黄、白三种颜色的小球,这些小球除颜色外没有其他差别,因为小张对取出一只红球没有把握,所以小张说:“从袋中取出一只红球的概率是50%”
(3)小李说,这次考试我得90分以上的概率是200%
(4)“从盒中取出一只红球的概率是0”,这句话是说取出一只红球的可能性很小
A. 3 B. 2 C. 1 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两队进行拔河比赛,裁判员让两队队长用“石头、剪子、布”的手势方式选择场地位置.规则是:石头胜剪子,剪子胜布,布胜石头,手势相同再决胜负.请你说明裁判员的这种作法对甲、乙双方是否公平,为什么?(用树状图或列表法解答)
相关试题

