【题目】滨海长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,已知行李质量为20kg时需付行李费2元,行李质量为50kg时需付行李费8元.
(1)当行李的质量x超过规定时,求y与x之间的函数表达式.
(2)求旅客最多可免费携带行李的质量.
参考答案:
【答案】(1)y=![]() x-2;(2)10kg
x-2;(2)10kg
【解析】
(1)根据(20,2)、(50,8)利用待定系数法,即可求出当行李的质量x超过规定时,y与x之间的函数表达式;
(2)令y=0,求出x值,此题得解.
解:(1)设y与x的函数表达式为y=kx+b.
将(20,2)、(50,8)代入y=kx+b中,得 ![]() ,
,
解得: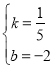 ,
,
∴当行李的质量x超过规定时,y与x之间的函数表达式为y=![]() x-2;
x-2;
(2)当y=0时,即![]() x-2=0,
x-2=0,
解得:x=10.
答:旅客最多可免费携带行李10kg.
-
科目: 来源: 题型:
查看答案和解析>>【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2),C(3,﹣3).
(1)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1.
(2)请画出与△ABC关于y轴对称的△A2B2C2.
(3)请写出A1、A2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题12分)某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为
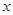 (米),与桌面的高度为
(米),与桌面的高度为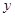 (米),运行时间为
(米),运行时间为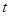 (秒),经多次测试后,得到如下部分数据:
(秒),经多次测试后,得到如下部分数据: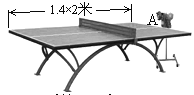
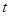 (秒)
(秒)0
0.16
0.2
0.4
0.6
0.64
0. 8
…
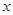 (米)
(米)0
0.4
0.5
1
1.5
1.6
2
…
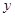 (米)
(米)0.25
0.378
0.4
0.45
0.4
0.378
0.25
…
(1)当
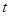 为何值时,乒乓球达到最大高度?
为何值时,乒乓球达到最大高度?(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,
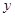 与
与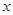 满足
满足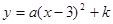
①用含
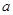 的代数式表示
的代数式表示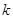 ;
;②球网高度为0.14米,球桌长(1.4×2)米,若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求
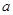 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为1的正方形,且DE=
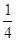 ,△ABF是△ADE的旋转图形
,△ABF是△ADE的旋转图形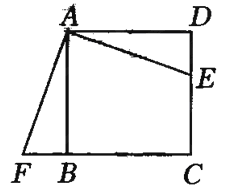
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连结EF,那么△AEF是怎样的三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC=AD,AD∥BC,
(1)求证:BD平分∠ABC;
(2)若∠C=78°,求∠D的度数.

相关试题

