搜索
【题目】如图，PA切⊙于点A，OP交⊙O于点B，且点B为OP的中点，弦AC∥OP．若OP=2，则图中阴影部分的面积为（ ）
A.
B.
C.
D.
参考答案：
【答案】C
【解析】解：连结OA、OC，如图，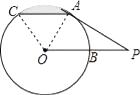
∵PA切⊙于点A，∴OA⊥PA，∴∠OAP=90°，
∵点B为OP的中点，∴OB=PB，∴OA= 
OP=1，
∴∠P=30°，∠POA=60°，
∵AC∥OP，∴∠OAC=∠POA=60°，
而OA=OC，∴△OAC为等边三角形，∴∠AOC=60°，
∴图中阴影部分的面积=S扇形AOC﹣S△AOC= 
．
故选C．
【考点精析】关于本题考查的扇形面积计算公式，需要了解在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以△ABC的BC边上一点O为圆心，经过A，C两点且与BC边交于点E，点D为CE的下半圆弧的中点，连接AD交线段EO于点F，若AB=BF．
（1）求证：AB是⊙O的切线；
（2）若CF=4，DF=
，求⊙O的半径r及sinB． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知抛物线y=x2+bx+c过A，B，C三点，点A的坐标是（3，0），点C的坐标是（0，﹣3），动点P在抛物线上．
（1）b= ， c= ， 点B的坐标为；（直接填写结果）
（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；
（3）过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，长方形纸片ABCD，AB=a，BC=b，且b＜a＜2b，则∠ADC的平分线DE折叠纸片，点A落在CD边上的点F处，再沿∠BEF的平分线EG折叠纸片，点B落在EF边上的点H处，则四边形CGHF的周长是（ ）
A.2a
B.2b
C.2（a﹣b）
D.a+b -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
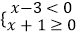（m＞0）与x轴交于A，B两点，点A在点B的左边，C是抛物线上一个动点（点C与点A，B不重合），D是OC的中点，连结BD并延长，交AC于点E，则 
的值是（ ）
A.
B.
C.
D. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB为⊙O的直径，C为⊙O上一点，弦AD平分∠BAC，交BC于点E，AB=10，AD=8，则AE的长为
-
科目： 来源： 题型：
查看答案和解析>>【题目】有这样一个数字游戏：将1，2，3，4，5，6，7，8，9这九个数字分别填在如图所示的九个空格中，要求每一行从左到右的数字逐渐增大，每一列从上到下的数字也逐渐增大．当数字3和4固定在图中所示的位置时，x代表的数字是 ， 此时按游戏规则填写空格，所有可能出现的结果共有种．
相关试题
