Question

【题目】如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．

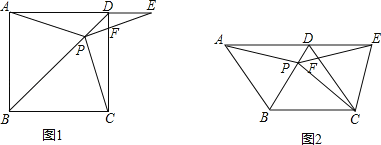
（1）证明：PC=PE；

（2）求∠CPE的度数；

（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．

Answer 1

【答案】（1）见解析；（2）∠CPF=90°；（3）AP=CE，见解析

【解析】（1）证明：在正方形ABCD中，AB=BC，

∠ABP=∠CBP=45°，

在△ABP和△CBP中，

，

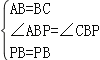∴△ABP≌△CBP（SAS），

∴PA=PC，

∵PA=PE，

∴PC=PE；

（2）由（1）知，△ABP≌△CBP，

∴∠BAP=∠BCP，

∴∠DAP=∠DCP，

∵PA=PE，

∴∠DAP=∠E，

∴∠DCP=∠E，

∵∠CFP=∠EFD（对顶角相等），

∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E，

即∠CPF=∠EDF=90°；

（3）在菱形ABCD中，AB=BC，∠ABP=∠CBP=60°，

在△ABP和△CBP中，

，

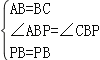∴△ABP≌△CBP（SAS），

∴PA=PC，∠BAP=∠BCP，

∵PA=PE，

∴PC=PE，

∴∠DAP=∠DCP，

∵PA=PC，

∴∠DAP=∠AEP，

∴∠DCP=∠AEP

∵∠CFP=∠EFD（对顶角相等），

∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP，

即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°，

∴△EPC是等边三角形，

∴PC=CE，

∴AP=CE．