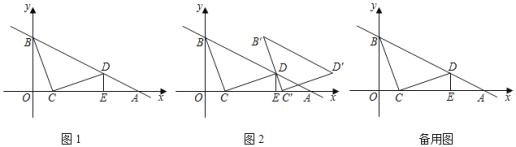
【题目】如图1,在平面直角坐标系中,直线y=-![]() x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)见解析(2)![]() (3)存在,点P的坐标为(0,
(3)存在,点P的坐标为(0,![]() )或(0,
)或(0,![]() )
)
【解析】
(1)利用同角的余角相等可得出∠OBC=∠ECD,由旋转的性质可得出BC=CD,结合∠BOC=∠CED=90°即可证出△BOC≌△CED(AAS);
(2)利用一次函数图象上点的坐标特征可求出点B的坐标,设OC=m,则点D的坐标为(m+3,m),利用一次函数图象上点的坐标特征可求出m值,进而可得出点C,D的坐标,由点B,C的坐标,利用待定系数法可求出直线BC的解析式,结合B′C′∥BC及点D在直线B′C′上可求出直线B′C′的解析式,再利用一次函数图象上点的坐标特征可求出点C′的坐标,结合点C的坐标即可得出△BCD平移的距离;
(3)设点P的坐标为(0,m),点Q的坐标为(n,-![]() n+3),分CD为边及CD为对角线两种情况考虑,利用平行四边形的对角线互相平分,即可得出关于m,n的二元一次方程组,解之即可得出点P的坐标.
n+3),分CD为边及CD为对角线两种情况考虑,利用平行四边形的对角线互相平分,即可得出关于m,n的二元一次方程组,解之即可得出点P的坐标.
(1)证明:∵∠BOC=∠BCD=∠CED=90°,
∴∠OCB+∠OBC=90°,∠OCB+∠ECD=90°,
∴∠OBC=∠ECD.
∵将线段CB绕着点C顺时针旋转90°得到CD,
∴BC=CD.
在△BOC和△CED中,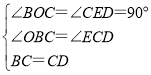 ,
,
∴△BOC≌△CED(AAS).
(2)解:∵直线y=-![]() x+3与x轴、y轴相交于A、B两点,
x+3与x轴、y轴相交于A、B两点,
∴点B的坐标为(0,3),点A的坐标为(6,0).
设OC=m,
∵△BOC≌△CED,
∴OC=ED=m,BO=CE=3,
∴点D的坐标为(m+3,m).
∵点D在直线y=-![]() x+3上,
x+3上,
∴m=-![]() (m+3)+3,解得:m=1,
(m+3)+3,解得:m=1,
∴点D的坐标为(4,1),点C的坐标为(1,0).
∵点B的坐标为(0,3),点C的坐标为(1,0),
∴直线BC的解析式为y=-3x+3.
设直线B′C′的解析式为y=-3x+b,
将D(4,1)代入y=-3x+b,得:1=-3×4+b,解得:b=13,
∴直线B′C′的解析式为y=-3x+13,
∴点C′的坐标为(![]() ,0),
,0),
∴CC′=![]() -1=
-1=![]() ,
,
∴△BCD平移的距离为![]() .
.
(3)解:设点P的坐标为(0,m),点Q的坐标为(n,-![]() n+3).
n+3).
分两种情况考虑,如图3所示:
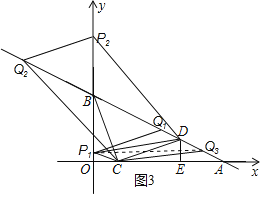
①若CD为边,当四边形CDQP为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,-![]() n+3),
n+3),
∴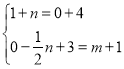 ,解得:
,解得: 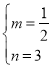 ,
,
∴点P1的坐标为(0,![]() );
);
当四边形CDPQ为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,-![]() n+3),
n+3),
∴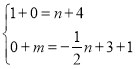 ,解得:
,解得: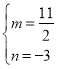 ,
,
∴点P2的坐标为(0,![]() );
);
②若CD为对角线,∵C(1,0),D(4,1),P(0,m),Q(n,-![]() n+3),
n+3),
∴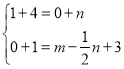 ,解得:
,解得: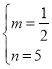 ,
,
∴点P的坐标为(0,![]() ).
).
综上所述:存在,点P的坐标为(0,![]() )或(0,
)或(0,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
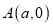 ,
,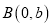 ,将线段
,将线段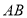 沿着
沿着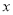 轴向右平移至
轴向右平移至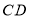 ,使点
,使点 与点
与点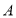 对应,点
对应,点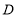 与点
与点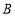 对应,连接
对应,连接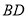 .
.(1)若
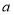 ,
,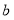 满足
满足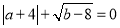 .
.①填空:
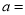 _______,
_______,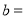 _______;
_______;②若面积关系
 成立,则点
成立,则点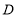 的坐标为_______;
的坐标为_______;(2)
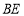 平分
平分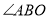 ,
, 平分
平分 ,
,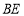 ,
, 相交于点
相交于点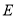 ,判断
,判断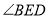 的大小,并说明理由.
的大小,并说明理由.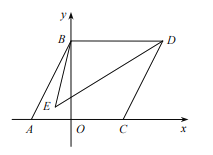
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE//AD,若AC=2,CE=4,则四边形ACEB的周长为 ▲ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 -(+3.7)+(+
-(+3.7)+(+ )-(-1.7) (2)(-72)×2
)-(-1.7) (2)(-72)×2 ×(-
×(- )÷(-3
)÷(-3 )
)(3)(
 -
- -
- +
+ )×(-24) (4)-32×(-2)+42÷(-2)3-∣-22∣
)×(-24) (4)-32×(-2)+42÷(-2)3-∣-22∣ -
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
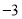
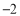
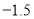
0
1
2.5
筐数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)
-
科目: 来源: 题型:
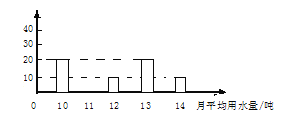
查看答案和解析>>【题目】为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况做一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨)并将调查结果制成了如图所示的条形统计图。
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计市直机关500户家庭中平均用水量不超过12吨的约有多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空并解答:
规定:a2=a×a,a3=a×a×a,an=a×a×…×a(n 个 a)
(1)(2×3)2= ,22×32= ,你发现(2× 3)2 的值与 22×32 的值 .
(2)(2×3)3= ,23×33= ,你发现(2×3)3 的值与 23×33 的值 .
由此,我们可以猜想:(a×b)2 a2×b2,(a×b)3 a3×b3,…(a×b)n an×bn.
(3)利用(2)题结论计算(﹣2)2018×(﹣
 )2019 的值.
)2019 的值.
相关试题

