Question

【题目】如图，在△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，动点P从点C出发，按C→B→A的路径，以2cm每秒的速度运动，设运动时间为t秒．

（1）当t＝1s时，求△ACP的面积．

（2）t为何值时，线段AP是∠CAB的平分线？

（3）请利用备用图2继续探索：当△ACP是等腰三角形时，求t的值．

Answer 1

【答案】（1）6；（2）；（3）3s或6s或s或5.4s．

【解析】

（1）当t＝1s时，△ACP是直角三角形，根据公式求△ACP的面积；

（2）如图3，过P作PH⊥AB于H，Rt△PHB中，PB＝8﹣2t，根据勾股定理列方程可求解；

（3）分四种情况进行讨论：①如图4，根据AC＝CP列式求解；②如图5，根据AC＝AP列式求解；③如图6，AP＝PC，根据AP＝PB列式求解；④如图7，AC＝CP，根据AP的值列式求解．

解：（1）如图1，点P在BC上，

由题意得：CP＝2t，

当t＝1时，PC＝2，

∴S△ACP＝ACPC＝×6×2＝6；

（2）如图2，

Rt△ACB中，由勾股定理得：AB＝＝10，

如图3，AP平分∠CAB，

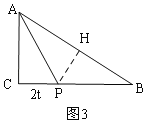
过P作PH⊥AB于H，

∵∠C＝90°，

∴PC＝PH＝2t，

∵∠C＝∠AHP＝90°，AP＝AP，

∴△ACP≌△AHP，

∴AH＝AC＝6，

∴BH＝4，

在Rt△PHB中，PB＝8﹣2t，

∴(2t)2+42＝(8﹣2t)2，

t＝；

则当t＝时，线段AP是∠CAB的平分线；

（3）当△ACP是等腰三角形时，有四种情况：

①如图4，AC＝CP时，

由题意得

2t＝6，

∴t＝3；

②如图5，AC＝AP时，

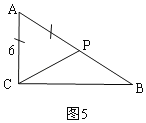
由题意得

18﹣2t＝6，

∴t＝6；

③如图6，AP＝PC时，

过P作PG⊥AC于G，

∵∠C＝90°，

∴PG∥BC，

∴AP＝PB，

即18﹣2t＝2t﹣8，

∴t＝；

④如图7，AC＝CP时，

过C作CM⊥AB于M，

∴AM＝PM=(18-2t)=9-t，

∵AB×CM=AC×BC，

∴CM=4.8，

∴AM==3.6，

∴9-t=3.6，

∴t＝5.4，

综上所述，当△ACP是等腰三角形时，t的值是3s或6s或s或5.4s．