【题目】正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.

(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
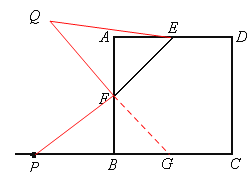
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全图形,并直接写出EF、EQ、BP三者之间的数量关系: .
参考答案:
【答案】解:(1)垂直且相等。
(2)EF、EQ、BP三者之间的数量关系为:![]() 。
。
证明如下:
如图,取BC的中点G,连接FG,
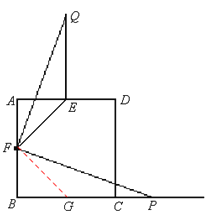
由(1)得EF=FG,EF⊥FG,
根据旋转的性质,FP=FQ,∠PFQ =90°。
∴∠GFP=∠GFE—∠EFP=90°—∠EFP,
∠EFQ=∠PFQ—∠EFP=90°—∠EFP。
∴∠GFP=∠EFQ。
在△FQE和△FPG中,∵EF=GF,∠EFQ=∠GFP,FQ = FP,
∴△FQE≌△FPG(SAS)。∴EQ=GP。
∴![]() 。
。
(3)补图如下,F、EQ、BP三者之间的数量关系为:![]() 。
。
【解析】
试题分析:(1)EF与FG关系为垂直且相等(EF=FG且EF⊥FG)。证明如下:
∵点E、F、G分别是正方形边AD、AB、BC的中点,
∴△AEF和△BGD是两个全等的等腰直角三角形。
∴EF=FG,∠AFE=∠BFG=45°。∴∠EFG=90°,即EF⊥FG。
(2)取BC的中点G,连接FG,则由SAS易证△FQE≌△FPG,从而EQ=GP,因此![]() 。
。
(3)同(2)可证△FQE≌△FPG(SAS),得EQ=GP,因此,
![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的底和腰是方程x2﹣7x+10=0的两根,则这个三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m﹣3)2+n2﹣6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.

(1)求m、n的值并写出A、B、C三点的坐标;
(2)若OF+BE=AB,求证:CF=CE. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值. 解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)a2+b2﹣4a+4=0,则a= . b= .
(2)已知x2+2y2﹣2xy+6y+9=0,求xy的值.
(3)已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2﹣4a﹣6b+11=0,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一天,王明和李玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 .
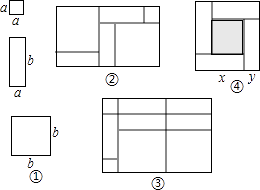
(1)图③可以解释为等式:
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图①所示的块,块,块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式: 1)xy=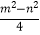 (2)x+y=m(3)x2﹣y2=mn(4)x2+y2=
(2)x+y=m(3)x2﹣y2=mn(4)x2+y2= 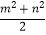
其中正确的有
A.1个
B.2个
C.3个
D.4个. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G.求证:

(1)DF∥BC;
(2)FG=FE. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,中国高铁发展迅速,高铁技术不断走出国门,成为展示我国实力的新名片.预计到2015年底,中国高速铁路营运里程将达到18000公里.将18000用科学记数法表示应为( )
A.18×103
B.1.8×103
C.1.8×104
D.1.8×105
相关试题

