【题目】如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m﹣3)2+n2﹣6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点. 
(1)求m、n的值并写出A、B、C三点的坐标;
(2)若OF+BE=AB,求证:CF=CE.
参考答案:
【答案】
(1)解:将(m﹣3)2+n2=6n﹣9变形得:(m﹣3)2+(n﹣3)2=0,
∴m=3,n=3,
∴A(3,3),B(3,0),C(0,3)
(2)解:∵OF+BE=AB,AE+EB=AB,
∴AE=OF,
∵四边形ABCD为正方形,
∴AC=OC,∠A=∠COF=90°,
在△ACE和△OCF中,
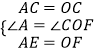 ,
,
∴△ACE≌△OCF(SAS),
∴CF=CE;
【解析】(1)已知等式变形后,利用非负数的性质求出m与n的值,即可确定出A,B,C的坐标;(2)由AE+EB=AB,以及OF+BE=AB,得到AE=OF,根据四边形ABOC为正方形,得到CA=CO,且∠A=∠COF=90°,利用SAS得到三角形ACE与三角形OCF全等,利用全等三角形对应边相等得到CF=CE;
-
科目: 来源: 题型:
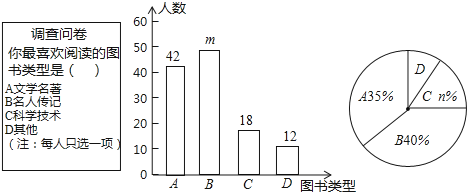
查看答案和解析>>【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程x2+4x+2=0配方后,原方程变形为( )
A. (x+4)2=2B. (x+2)2=2C. (x+4)2=-3D. (x+2)2=-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的底和腰是方程x2﹣7x+10=0的两根,则这个三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值. 解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)a2+b2﹣4a+4=0,则a= . b= .
(2)已知x2+2y2﹣2xy+6y+9=0,求xy的值.
(3)已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2﹣4a﹣6b+11=0,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.

(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全图形,并直接写出EF、EQ、BP三者之间的数量关系: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,王明和李玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 .
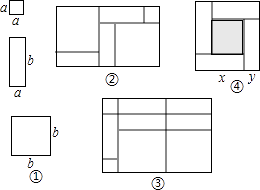
(1)图③可以解释为等式:
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图①所示的块,块,块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式: 1)xy=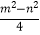 (2)x+y=m(3)x2﹣y2=mn(4)x2+y2=
(2)x+y=m(3)x2﹣y2=mn(4)x2+y2= 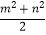
其中正确的有
A.1个
B.2个
C.3个
D.4个.
相关试题

