【题目】探究:如图①,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,过点P分别作AB、AD的平行线,交BC、CD于点M、N,求![]() 的值;
的值;
应用:如图②,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,Rt△PEF的两条直角边PE、PF分别交BC、CD于点M、N,则![]() = .
= .

参考答案:
【答案】![]() ;
;![]()
【解析】
试题分析:探究:首先证明PN=MC,由PM∥AB,推出![]() ,即
,即![]() ,由此即可解决问题.
,由此即可解决问题.
应用:先过P作PG⊥BC于G,作PH⊥CD于H,判定△PGM∽△PHN,再根据相似三角形的性质以及探究的结论即可解决问题;
试题解析:探究:解:如图①中,
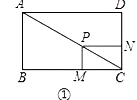
∵四边形ABCD是矩形,
∴∠B=∠DCB=90°,AD=BC=4
∵PM⊥BC,PN⊥CD,
∴∠PMC=∠PNC=90°,
∴四边形PMCN是矩形,
∴PC=CM,
∵∠PMC=∠B=90°,
∴PM∥AB,
∴△CPM∽△CAB,
∴![]() ,即
,即![]() ,
,
∵AB=3,BC=4
∴![]() =
=![]()
应用:解:如图②中,过P作PG⊥BC于G,作PH⊥CD于H,则∠PGM=∠PHN=90°,∠GPH=90°,

∵Rt△PEF中,∠FPE=90°
∴∠GPM=∠HPN
∴△PGM∽△PHN
∴![]() ,
,
由条件可知,![]() =
=![]() ,
,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
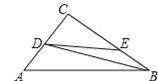
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C﹣A﹣B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为t(s)(0<t<8).
(1)求AB的长;
(2)当△BDE是直角三角形时,求t的值;
(3)设△CDE的面积为y(cm2),求y与t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在电子显微镜下测得一个圆球体细胞的直径是5×10-5 cm,2×103个这样的细胞排成的细胞链的长是________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a为正整数,且x2a=6,则(2x5a)2÷4x6a的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.5x2x3=5x5
B.2x+3y=5xy
C.4x8÷2x2=4x4
D.(﹣x3)2=x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,必然事件是( )
A.抛掷1个均匀的骰子,出现6点向上
B.两直线被第三条直线所截,同位角相等
C.366人中至少有2人的生日相同
D.实数的绝对值是非负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】在甲处劳动的有27人,在乙处劳动的有19人.现在另调20人去支援,使在甲处的人数为在乙处的人数的2倍,应调往甲、乙两处各多少人?
相关试题

