Question

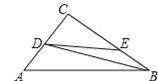
【题目】如图，在△ABC中，∠C=90°，AC=6cm，BC=8cm，点D从点C出发，以2cm/s的速度沿折线C﹣A﹣B向点B运动，同时，点E从点B出发，以1cm/s的速度沿BC边向点C运动，设点E运动的时间为t（s）（0＜t＜8）．

（1）求AB的长；

（2）当△BDE是直角三角形时，求t的值；

（3）设△CDE的面积为y（cm2），求y与t的函数关系式．

Answer 1

【答案】（1）10（2）或（3）当0＜t≤3时，y=8t﹣t2；当3＜t＜8时，y=t2﹣t+

【解析】

试题分析：（1）直接利用勾股定理计算；

（2）当△BDE是直角三角形时，∠B不可能为直角，所以分两种情况讨论：i）图1，当∠BED=90°时；ii）图2，当∠EDB=90°时；利用相似求边，再利用同角三角函数值列等式计算求出t的值；

（3）分两种情况用三角形的面积公式求解即可．

试题解析：（1）由勾股定理得：AB==10，

（2）如图1，当∠BED=90°时，△BDE是直角三角形，

则BE=t，AC+AD=2t，

∴BD=6+10﹣2t=16﹣2t，

∵∠BED=∠C=90°，

∴DE∥AC，

∴，

∴，

∴DE=t，

∵sinB=，

∴，

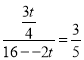t=；

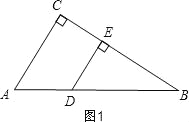
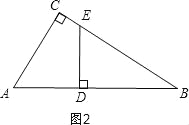
如图2，当∠EDB=90°时，△BDE是直角三角形，

则BE=t，BD=16﹣2t，

cosB=，

∴，

∴t=；

∴当△BDE是直角三角形时，t的值为或

（3）当0＜t≤3时，y=×2t×（8﹣t）=8t﹣t2；

当3＜t＜8时，y=（8﹣t）×（16﹣2t）=t2﹣t+．