Question

【题目】如图①的长方形ABCD中， E在AD上，沿BE将A点往右折成如图②所示，再作AF⊥CD于点F，如图③所示，若AB＝2，BC＝3，∠BEA＝60°，则图③中AF的长度为_______．

Answer 1

【答案】3－

【解析】

作AH⊥BC于H．证明四边形AFCH是矩形，得出AF=CH，在Rt△ABH中，求得∠ABH=30°，则根据勾股定理可求出BH=，可求出HC的长度即为AF的长度.

解：如下图，作AH⊥BC于H．则∠AHC=90°，

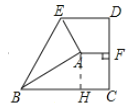
∵四边形形ABCD为长方形，

∴∠B=∠C=∠EAB=90°，

∵AF⊥CD，

∴∠AFC=90°，

∴四边形AFCH是矩形，

∵∠BEA＝60°，

∴∠EAB=30°，

∴根据折叠的性质可知∠AEH=90°-2∠EAB=30°，

∵在Rt△ABH中， AB=2,

∴,

根据勾股定理

∵BC=3,

∴.

故填：3－.