【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
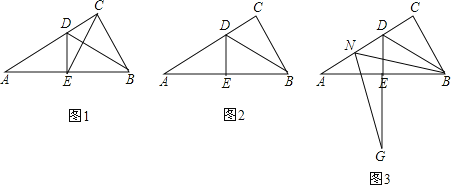
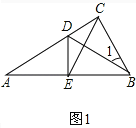
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)画图见解析,AD=DG+DM;(3)AD=DG﹣DN,理由见解析.
【解析】
试题分析:(1)利用“三边相等”的三角形是等边三角形证得△EBC是等边三角形;
(2)延长ED使得DW=DM,连接MN,即可得出△WDM是等边三角形,利用△WGM≌△DBM即可得出BD=WG=DG+DM,再利用AD=BD,即可得出答案;
(3)利用等边三角形的性质得出∠H=∠2,进而得出∠DNG=∠HNB,再求出△DNG≌△HNB即可得出答案.
(1)证明:如图1所示:
在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠ABC=60°,BC=![]() .
.
∵BD平分∠ABC,
∴∠1=∠DBA=∠A=30°.
∴DA=DB.
∵DE⊥AB于点E.
∴AE=BE=![]() .
.
∴BC=BE.
∴△EBC是等边三角形;
(2)结论:AD=DG+DM.
证明:
如图2所示:延长ED使得DW=DM,连接MW,
∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,
∴∠ADE=∠BDE=60°,AD=BD,
又∵DM=DW,
∴△WDM是等边三角形,
∴MW=DM,
在△NGM和△DBM中,
∵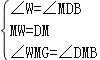
∴△WGM≌△DBM,
∴BD=WG=DG+DM,
∴AD=DG+DM.
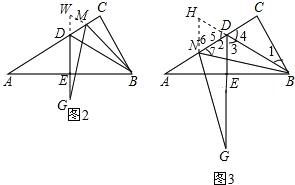
(3)结论:AD=DG﹣DN.
证明:延长BD至H,使得DH=DN.
由(1)得DA=DB,∠A=30°.
∵DE⊥AB于点E.
∴∠2=∠3=60°.
∴∠4=∠5=60°.
∴△NDH是等边三角形.
∴NH=ND,∠H=∠6=60°.
∴∠H=∠2.
∵∠BNG=60°,
∴∠BNG+∠7=∠6+∠7.
即∠DNG=∠HNB.
在△DNG和△HNB中,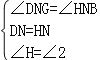
∴△DNG≌△HNB(ASA).
∴DG=HB.
∵HB=HD+DB=ND+AD,
∴DG=ND+AD.
∴AD=DG﹣ND.
-
科目: 来源: 题型:
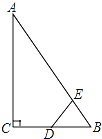
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】与数轴上的点一一对应的是
A. 整数 B. 有理数 C. 无理数 D. 实数
-
科目: 来源: 题型:
查看答案和解析>>【题目】求x值:
(1)5(x﹣1)2=125 (2)2x3=54.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区2012年屋顶绿化面积为2000平方米,计划2014年屋顶绿化面积要达到2880平方米,如果每年屋顶绿化面积的增长率相同,那么这个增长率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别是3cm和7cm,它的周长是____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
相关试题

