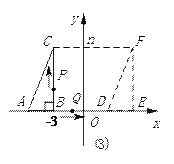
【题目】(12分)如图,直角三角形的顶点A、B在x轴上,ABC=90 ,BC//y轴,且C点在第二象限,B点为(-3,0),将直角三角形ABC沿x轴水平向右平移m个单位,得到对应的直角三角形DEF,其中点A、B、C分别对应点D、E、F,求:
(1)用含m的式子表示E点坐标及AD的长度;
(2)若C点为(-3,n),设四边形BEFC的周长为y,试用含m、n的式子表示周长y;
(3)在(2)的条件下,点P和点Q分别以1个单位/秒,2个单位/秒的速度同时从B点出发,其中,P点沿B→C→F→E→B的方向运动,Q点沿B→E→F→C→B的方向运动,相遇时则停止运动。当P点到达C点时,Q点恰到达E点;从B点出发起,6秒后P点与Q点相遇停止了运动,求四边形ADFC的面积。

参考答案:
【答案】(1) E点为(m -3,0),AD=m;(2) y = 2 m+2 n ; (3)18
【解析】试题分析:(1)由平移的性质即可得出答案;
(2)由矩形的性质得出BE=CF=m,BC=EF=n,即可得出答案;
(3)由题意得出m和n的方程组,解方程组求出m和n的值,即可得出答案.
试题解析:
(1):(1)∵B(-3,0),
∴OB=3,
∵直角三角形ABC沿x轴水平向右平移m个单位,得到对应的直角三角形DEF,
∴AD=BE=m,
∴OE=m-3,
∴E点为(m-3,0);
(2)易知,四边形BEFC为长方形,BE=CF= m,BC=EF= n
∴ y = 2 m+2 n
(3)由题意,得:
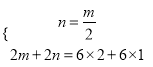
解这个方程组,得:
![]()
∴![]() ,
, ![]()
由平移知,四边形ADFC的面积=长方形BEFC的面积
∴四边形ADFC的面积![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】改写命题“对角线互相平分的四边形是平行四边形”:如果__________,那么_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数的图象如图所示,以下结论正确的是( )
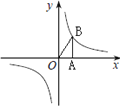
①常数m<1;
②y随x的增大而减小;
③若A为x轴上一点,B为反比例函数上一点,则S△ABC=
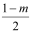 ;
;④若P(x,y)在图象上,则P′(-x,-y)也在图象上.
A.①②③ B.①③④ C.①②③④ D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图.
请根据统计图表提供的信息,解答下列问题:

(1)参加调查的人数共有 人;在扇形图中,m= ;将条形图补充完整;
(2)如果该校有3500名学生,则估计喜欢“篮球”的学生共有多少人?
(3)该社团计划从篮球、足球和乒乓球中,随机抽取两种球类组织比赛,请用树状图或列表法,求抽取到的两种球类恰好是“篮球”和“足球”的概率.
-
科目: 来源: 题型:
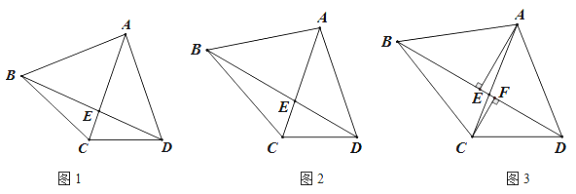
查看答案和解析>>【题目】在四边形ABCD中,AC、BD交于点E,且∠ACD=∠ADC.
(1)如图1,若AB=AD,求证:∠BAC=2∠BDC;
(2)如图2,在(1)的条件下,若∠BDC=30°,求证:BC=AC.
(3)如图3,若BC=AD,∠BDC=30°,过A作AE⊥BD于E,过C作CF⊥BD于F, 且EF:BE=2:11,DF=9,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC≌△DEF,∠A=80°,∠B=40°,那么∠F的度数是( )
A.80°
B.40°
C.60°
D.120°
相关试题

